设为首页
加入收藏
An Improvement of the Linearized Planetary Boundary Layer Parameterization Scheme for CMA-GFS 4DVar
-
摘要: 持续发展和优化切线性模式的线性化物理过程，保持与非线性模式一致是改善四维变分同化（4DVar）分析和预报效果的有效方法之一。目前业务系统的CMA-GFS模式采用基于Charney-Phillips（C-P）跳点的边界层参数化方案，而CMA-GFS 4DVar系统中采用基于Lorenz跳点的边界层线性化方案。为改善CMA-GFS 4DVar系统的边界层分析和预报效果，基于C-P跳点的边界层参数化方案研发了新边界层线性化方案，并通过对方案中地表热量通量和水汽通量扰动、自由大气的理查逊系数扰动、边界层的热量和动量交换系数扰动等进行更加精细地规约化约束，在确保CMA-GFS切线性和伴随模式稳定运行的情况下，减少线性化过程对切线性模式预报精度的影响。切线性近似试验检验表明：相较于原方案，新边界层线性化方案可以减少边界层位温和比湿的相对误差，最大可减少10%。批量4DVar循环同化试验表明：新边界层线性化方案可以有效改善切线性模式对低层位温、风场和比湿扰动的预报精度，减少4DVar内外循环目标泛函的相对差异，并提高700 hPa位势高度的可预报时效。Abstract: By continuously developing and optimizing the linearized physical process of the tangent linear model and keeping it consistent with the nonlinear model, the analysis and forecasting performance of four-dimensional variational data assimilation (4DVar) of China Meteorological Administration Global Forecast System (CMA-GFS) can be effectively improved. Currently, the planetary boundary layer (PBL) parameterization scheme adopted by CMA-GFS model is based on Charney-Phillips (C-P) grid, while the linearization PBL parameterization scheme used in CMA-GFS 4DVar is on the basis of Lorenz grid. The zigzag noise of the temperature and moisture in the boundary layer is removed and the correspondent profiles appear to be smooth with C-P PBL parameterization scheme, and the forecast errors of CMA-GFS model are effectively reduced. To improve the analysis and prediction effects of 4DVar on the boundary layer, a new linearized PBL parameterization scheme based on the C-P grid (TL_NMRF_CP) is developed. By making more refined regularization constraints on the disturbances of the surface heat flux, the surface water vapor flux, Richardson coefficient of the free atmosphere, the heat and momentum exchange coefficient of the boundary layer, the influence of the linearization process on the accuracy of the tangent linear approximation is reduced while ensuring stable operation of the tangent linear and adjoint models. Two tests are designed, one is TL_MRF test based on the original TL_MRF scheme and the other is TL_NMRF_CP test based on the TL_NMRF_CP scheme. The tangent linear approximation tests show that, compared with the original scheme, the TL_NMRF_CP scheme can improve the tangent linear model forecast accuracy on the boundary layer, reduce the relative error of the potential temperature of the boundary layer by up to 10%, reduce the relative error of the specific humidity by 5% at the most, and reduce the relative error of zonal wind by up to 12%. In the minimization process of CMA-GFS 4DVar, the TL_NMRF_CP scheme can reduce the relative difference of the cost functions caused by different resolutions between inner and outer loops of the 4DVar system, and improve the convergence efficiency of 4DVar. The batch cycle assimilation forecast experiments of CMA-GFS 4DVar further verify that the TL_NMRF_CP scheme can provide better analysis and prediction results. The TL_NMRF_CP scheme has also been applied to CMA-GFS 4DVar operation system.
-
引言
四维变分同化(four-dimensional variational data assimilation, 4DVar)方法的发展和实现是数值天气预报的重大突破之一，是三维变分同化在时间维度上的扩展，暗含了初始背景误差协方差在同化时间窗内的流依赖特征，是一种高效利用高时空分辨率卫星观测资料的成功方法之一[1-3]。目前，4DVar方法已在多个数值预报业务中心得到业务化应用[4-8]。为了满足4DVar业务化所需的计算时效，4DVar一般采用增量变分资料同化技术，在极小化过程中利用时间向前积分的切线性模式(tangent linear model，TLM)和时间向后积分的伴随模式(adjoint model，ADM)计算代价函数的目标泛函和梯度信息[9-10]。TLM是非线性模式的一阶近似，主要包含两大类线性化模块：动力框架和物理过程。动力框架主要描述大气大尺度演变特征，接近线性，其线性近似精确度较高。物理过程的空间尺度远小于模式动力框架的分辨率，需要采用参数化方法，因此具有强非线性和不连续的特点，如边界层物理过程复杂的湍流运动、湿物理过程强烈的垂直运动和微物理变换等。持续发展和优化线性化物理过程，保持与非线性模式一致是改善4DVar分析和预报效果的有效方法之一[11-13]。线性化物理过程的开发存在很多困难，如需要简化线性化物理过程中的强非线性项，以及解决线性化过程中大量判断语句带来的开关选项不连续问题等[14]，因此在线性化物理过程研发时需要对原物理过程参数化方案进行简化，并对线性化物理过程的相关参数扰动进行规约化处理，确保TLM和ADM计算的数值稳定性[11-15]。
近年中国数值预报自主创新发展取得显著进展，建立了以CMA-GFS和CMA-MESO(原GRA- PES，Global and Regional Assimilation PrEdiction system)为核心的数值预报业务体系[2, 16-19]。2018年基于CMA-GFS TLM和ADM发展的4DVar系统在中国气象局实现业务化[7]，包括增加两个湿线性化物理过程等[12-13]围绕CMA-GFS 4DVar分析预报效果的改善和优化工作持续进行。业务系统的CMA-GFS模式同样在持续发展和升级，其中关于边界层线性化物理过程优化和升级主要内容包括：CMA-GFS模式动力框架在垂直方向上考虑了Charney-Phillips(C-P)跳点的优势[20]，水平风变量分布在模式半层，温度、湿度和水物质变量分布在模式整层，而原边界层物理过程采用的NMRF(新MRF)方案则是基于Lorenz跳点进行计算[21-22]；为了解决边界层物理过程与动力框架垂直格点分布不一致问题，陈炯等[23-24]、张萌等[25]在CMA-GFS模式中研发了基于C-P跳点的NMRF边界层方案(NMRF_CP)，该方案消除了模式预报的边界层温度和湿度不合理的锯齿状振荡，使模式对边界层过程的描述更合理，有效减少了CMA-GFS模式预报误差。
目前，CMA-GFS 4DVar中的边界层线性化物理过程方案采用的是基于Lorenz跳点的MRF线性化方案(TL_MRF)[26-27]，为了与业务系统CMA-GFS非线性模式所采用的NMRF_CP方案保持一致，并进一步改善4DVar对边界层过程的分析和预报效果，本文研发了基于NMRF_CP方案的新边界层线性化方案(TL_NMRF_CP)，并对强非线性特征的平滑和线性化方案的规约化处理进行详细研究。在此基础上，通过试验比较TL_NMRF_CP方案与TL_MRF方案的切线性近似精度，评估两种方案对4DVar目标泛函相对差异的影响，并利用批量循环分析预报试验检验TL_NMRF_CP方案在4DVar中的分析和预报效果，为CMA-GFS模式业务化升级提供技术支撑。
1. TL_NMRF_CP方案简介
1.1 NMRF_CP方案
边界层参数化方案是数值预报模式物理过程参数化方案中非常重要的组成部分，它采用平均量描述次网格边界层通量，使大气运动方程闭合并进行求解。目前CMA-GFS模式采用NMRF边界层方案，该方案考虑一阶K闭合条件，使用K廓线闭合描述不稳定边界层中非局地扩散过程。相较于MRF方案，NMRF方案主要增加边界层层积云的辐射效应对湍流扩散的加强作用[26]，其方程可表示为
(1) 式(1)中，ψ代表模式物理量(如纬向风u、经向风v、位温θ和比湿q)，K为热动量扩散系数，γ表示大尺度涡对通量的贡献。
大气边界层的湍流活动旺盛且交换强烈，是边界层过程的主要部分，对模式预报影响很大；自由大气中的湍流活动相对较弱，但局地可能出现强烈的湍流活动。式(1)的关键是如何分别计算边界层和自由大气中的扩散系数K，一般通过大气廓线计算，
CMA-GFS模式动力框架在垂直方向采用C-P跳点方案，纬向风u和经向风v位于模式半层，位温θ和比湿q位于模式整层。NMRF_CP方案考虑到水平风和温度不在同一垂直层次的特点，采用温度相关量插值到半层计算整层理查逊系数Ri，得到整层热量和动量扩散系数K，通过线性插值得到半层热量扩散系数，可以消除模式预报的边界层温度和湿度不合理的锯齿状振荡，使模式对边界层过程的描述更合理[23-24]。
1.2 TL_NMRF_CP方案
边界层参数化方程(式(1))的切线性方程为
(2) 式(2)中，ψ′代表模式物理量ψ的扰动(如u的扰动u′，v的扰动v′，θ的扰动θ′和q的扰动q′)，扩散系数K的扰动
TL_NMRF_CP方案代码是根据NMRF_CP代码直接编写的，由此得到的切线性方案经常导致TLM异常增长。为了阻止TLM的异常增长，本文分别参考ECMWF边界层方案中阻止异常扰动的方法[11]和CMA-GFS TLM针对MRF线性化方案中阻止异常扰动的方法(忽略地表动量通量、热量通量和扩散系数的扰动)[27]。根据TL_NMRF_CP方案在CMA-GFS模式中的具体实现方案，通过试验确认TL_NMRF_CP方案对切线性量采用的规约化约束处理方法，并与TL_MRF方案的规约化方法进行对比。TL_NMRF_CP的规约化处理方法比TL_MRF更加精细，TL_MRF方案中直接忽略了相关变量扰动(如地表热通量和水汽通量扰动，自由大气的理查逊系数Ri的扰动R′i, 边界层热量和动量扩散系数的扰动K′，模式最底层的风和温度扰动)，TL_NMRF_CP方案中针对这些变量进行更加精细的规约化约束(地表热通量和水汽通量扰动缩小到0.1倍，R′i缩小到0.01倍，K′和模式最底层风扰动缩小到0.5倍，忽略模式最底层的温度扰动)，在确保切线性模式稳定积分的情况下，边界层切线性预报近似取得更好效果。
2. TL_NMRF_CP方案在CMA-GFS TLM中的评估
2.1 试验设置
本节所采用的模式版本为CMA-GFS业务化版本(CMA-GFS V3.0)，其水平分辨率为1.0°×1.0°，垂直方向为87层，预报时间为6 h，积分步长为600 s。试验初始扰动场采用CMA-GFS 4DVar循环同化系统(CMA-GFS V3.0版本，水平分辨率为0.25°×0.25°，垂直分为87层)提供的分析增量δx(δx=xa-xb)，其中背景场xb是根据三维插值方法将模式6 h预报场由0.25°插值成1.0°，分析场xa是将同化分析场由0.25°插值成1.0°。非线性扰动试验设置为由包含全物理过程的CMA-GFS非线性模式从两个不同初始条件起报得到的6 h预报场的差值，其中一个以背景场xb起报，另一个以分析场xa起报。切线性扰动试验的模式轨迹是由包含全物理过程的CMA-GFS非线性模式以背景场xb为初始场计算的。选择不同日期的个例(北半球夏季个例是2019年6月1日，北半球冬季个例是2019年12月1日)测试TL_NMRF_CP在CMA-GFS TLM中的切线性近似效果，并与TL_MRF方案进行比较。作为参考试验的非线性模式扰动计算采用全物理过程，TLM扰动试验则采用简化的线性化物理过程，包括次网格尺度地形参数化方案、边界层垂直扩散方案、积云深对流和大尺度凝结[13]。
本节设计两组试验。①TL_MRF试验：基于上文TLM设置，TLM的边界层线性化方案采用默认的Lorenz跳点的TL_MRF方案；②TL_NMRF_CP试验：基于上文TLM设置，TLM的边界层线性化方案采用本文研发的C-P跳点的TL_NMRF_CP方案。
2.2 线性化物理过程的诊断方法
本文采用定量方式诊断线性化物理过程对TLM预报效果的影响。参考试验的非线性扰动预报为两个不同初始条件xa和xb起报的非线性模式预报的差值，即ΔM(δx)=M(xa)-M(xb)，相应需要对比测试的切线性扰动预报为L(δx)，M为非线性模式，L为切线性模式。切线性近似效果的诊断方法是比较切线性扰动预报L(δx)与非线性扰动预报ΔM(δx)的绝对误差[11-12]：
(3) ε需要针对每个模式变量在每个模式层和格点上进行计算。绝对误差ε相对于ΔM(δx)的相对误差计算公式为
(4) 为了进一步分析不同线性化物理过程对TLM的改善效果，比较两个切线性扰动预报(L2(δx)，L1(δx))与非线性扰动预报ΔM(δx)的绝对误差减少量(|L2(δx)-ΔM(δx)|-|L1(δx)-ΔM(δx)|)的纬向平均分布，如果误差减少量小于0，表示L2(δx)的切线性近似效果好于L1(δx)。
2.3 TL_NMRF_CP方案的切线性近似评估
2.3.1 位温扰动切线性近似评估
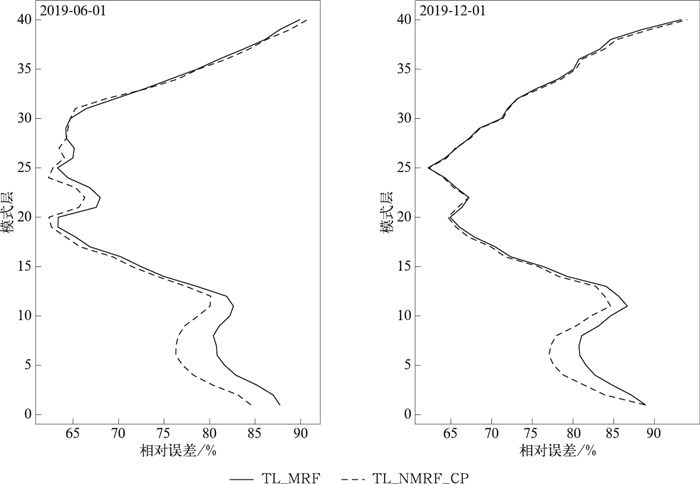
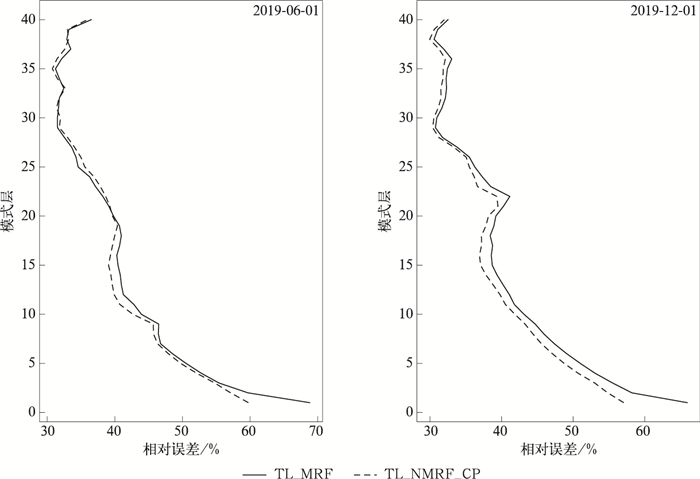
根据式(4)计算TL_NMRF_CP试验和TL_MRF试验全球平均位温扰动相对误差的垂直分布(图 1)。由图 1可见，对于2019年6月1日个例，相较于TL_MRF试验，TL_NMRF_CP试验在模式9层(约560 m高度)以下的位温扰动切线性近似预报效果得到有效改善，并且越接近模式低层改善越明显，相对误差最大可减少12%，为了阻止TL_NMRF_CP方案误差的异常增长，对模式底层温度扰动的规约化处理方案导致位温扰动切线性近似在模式9~15层(大约560~1500 m高度)略有负效果，这对于TL_NMRF_CP规约化处理方案是可以接受的。对于2019年12月1日个例，TL_NMRF_CP试验在模式14层(约1360 m高度)以下的位温扰动切线性近似预报效果比TL_MRF试验更优，TL_NMRF_CP试验对模式低层的改善程度比较接近，相对误差约能减少7%。
![]()
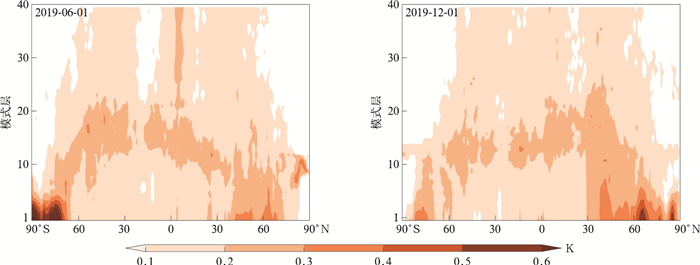
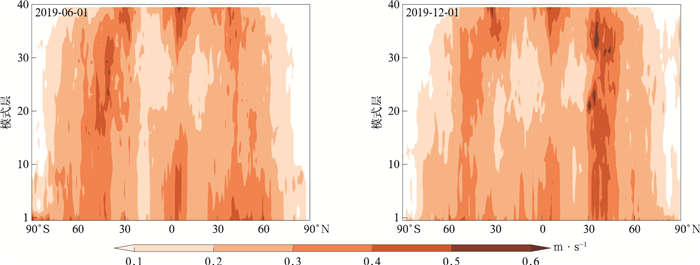
图 1 CMA-GFS切线性模式全球平均位温扰动相对误差垂直分布Figure 1. Vertical distribution of global mean relative error of potential temperature perturbation in CMA-GFS tangent linear model根据式(3)计算TL_MRF试验纬向平均的位温扰动绝对误差如图 2所示，图 3是TL_NMRF_CP试验相对于TL_MRF试验的位温扰动绝对误差减少量的纬向平均。对于2019年6月1日个例，TL_NMRF_CP试验的切线性近似在南极附近改善最为显著(图 3)，原因之一是TL_MRF试验在此处的位温扰动绝对误差比较大(图 2)；TL_NMRF_CP试验在北半球中高纬度低层也略有改善(图 3)。对于2019年12月1日个例，TL_NMRF_CP试验切线性近似同样在南极附近改善最为显著(图 3)，但TL_MRF试验在此处的位温扰动绝对误差(图 2)没有2019年6月1日个例(图 2)明显；与2019年6月1日个例类似，TL_NMRF_CP试验在北半球中高纬度低层也略有改善(图 3)。总之，基于C-P跳点开发的TL_NMRF_CP边界层线性化方案能够有效提高CMA-GFS TLM边界层位温扰动的预报精度。
![]()
图 2 TL_MRF试验的位温扰动纬向平均绝对误差Figure 2. Zonal mean absolute errors of potential temperature perturbation for TL_MRF test![]()
图 3 TL_NMRF_CP试验位温扰动相对于TL_MRF试验的改善Figure 3. Improvements in potential temperature perturbation of TL_NMRF_CP test relative to TL_MRF test2.3.2 比湿扰动切线性近似评估
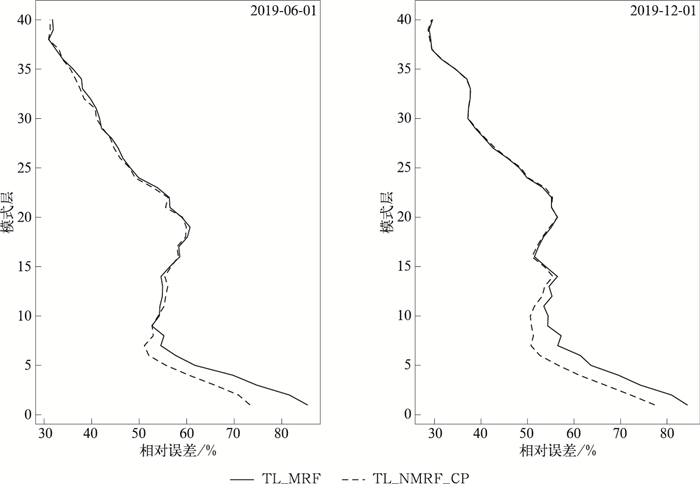
图 4是根据式(4)计算的TL_NMRF_CP试验和TL_MRF试验的全球平均比湿扰动相对误差的垂直分布。由图 4可见，对于2019年6月1日个例，相较于TL_MRF试验，TL_NMRF_CP试验在模式28层(约5000 m高度)以下的比湿扰动切线性近似预报效果得到有效改善，其中模式第5层(约200 m高度)的改善最为显著，相对误差可减少约5%；对于2019年12月1日个例，在模式14层(约1360 m高度)以下，TL_NMRF_CP试验的比湿扰动切线性近似预报效果较TL_MRF试验好，同样在模式第5层改善最为显著，相对误差可减少约5%。
![]()
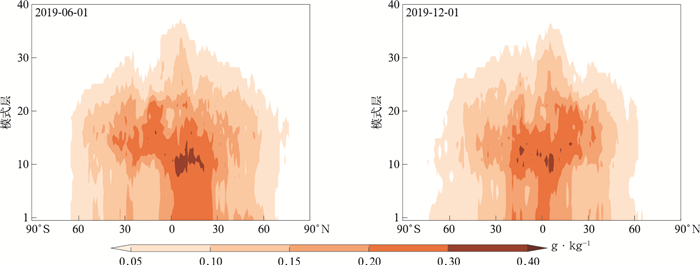
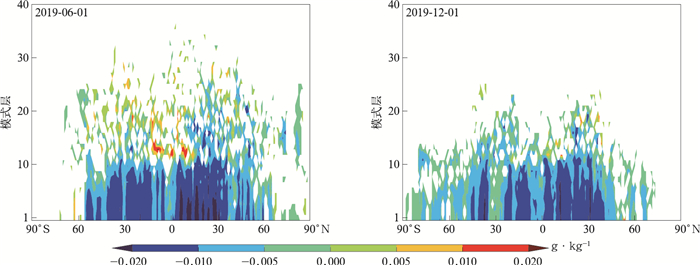
图 4 CMA-GFS切线性模式全球平均比湿扰动相对误差垂直分布Figure 4. Vertical distribution of global mean relative error of specific humidity perturbation in CMA-GFS tangent linear model根据式(3)计算TL_MRF试验纬向平均的比湿扰动绝对误差如图 5所示，图 6是TL_NMRF_CP试验相对于TL_MRF试验比湿扰动绝对误差减少量的纬向平均。由图 5和图 6可见，对于这两个个例，TL_NMRF_CP试验切线性近似均在南北半球中低纬度和热带边界层附近改善显著。由此可见，基于C-P跳点开发的TL_NMRF_CP边界层方案能够有效提高CMA-GFS TLM边界层比湿扰动的预报精度。
![]()
图 5 TL_MRF试验的比湿扰动纬向平均绝对误差Figure 5. Zonal mean absolute errors of specific humidity perturbation for TL_MRF test![]()
图 6 TL_NMRF_CP试验比湿扰动相对于TL_MRF试验的改善Figure 6. Improvements in specific humidity perturbation of TL_NMRF_CP test relative to TL_MRF test2.3.3 纬向风扰动切线性近似
图 7是根据式(4)计算的TL_NMRF_CP试验和TL_MRF试验全球平均纬向风扰动相对误差的垂直分布。由图 7可见，相较于TL_MRF试验，TL_NMRF_CP试验纬向风扰动切线性近似在模式低层改善最为明显，相对误差最大可减少约10%。
![]()
图 7 CMA-GFS切线性模式全球平均纬向风扰动相对误差垂直分布Figure 7. Vertical distribution of global mean relative error of zonal wind perturbation in CMA-GFS tangent linear model根据式(3)计算TL_MRF试验纬向平均纬向风的扰动绝对误差如图 8所示，图 9是TL_NMRF_CP试验相对于TL_MRF试验纬向平均纬向风扰动绝对误差减少量。由图 8和图 9可见，对于这两个个例，TL_NMRF_CP试验切线性近似均在南半球高纬度区域(和位温扰动的改善位置一致)以及模式最低层附近有明显改善。由此可见，基于C-P跳点开发的TL_NMRF_CP方案能够有效提高CMA-GFS TLM边界层纬向风扰动的预报精度。
![]()
图 8 TL_MRF试验的纬向风扰动纬向平均绝对误差Figure 8. Mean absolute errors of zonal wind perturbation for TL_MRF test![]()
图 9 TL_NMRF_CP试验纬向风扰动相对于TL_MRF试验的改善Figure 9. Improvements in zonal wind perturbation of TL_NMRF_CP test relative to TL_MRF test综上所述，在CMA-GFS TLM的切线性近似评估中，相较于TL_MRF方案，基于C-P跳点开发的TL_NMRF_CP方案可有效改善TLM对边界层的预报精度，主要原因是基于C-P跳点开发的TL_NMRF_CP方案与CMA-GFS非线性模式的边界层物理过程的一致性更高，能更好模拟非线性模式边界层扰动的发展。
3. TL_NMRF_CP方案在CMA-GFS 4DVar中的评估
3.1 评估方法
一般地，4DVar的目标泛函定义为
(5) 式(5)中，上标T表示矩阵转置，上标-1表示矩阵的逆。xa和xb是由模式变量构成的列向量，分别代表分析场和背景场，二者均位于4DVar时间窗的初始时刻。B是背景场的误差协方差矩阵，下标i表示不同时刻，y是观测构成的列向量，M0→i表示从初始时刻t0到观测时刻ti的预报模式积分，H是观测算子，它将模式变量转换成观测相当量，R是观测的误差协方差矩阵。
4DVar通过迭代算法求解目标泛函的极小化问题。由于极小化算法需要目标泛函及其梯度的值，而4DVar的目标泛函和梯度的计算均涉及模式积分，计算量巨大，因此实际应用中通常采用增量分析方案[8]。该方案假定观测算子和预报模式满足线性近似
(6) 其中，δx=xa-xb，δHi是观测算子Hi的切线性算子，L0→i是非线性预报模式M0→i对应的切线性模式。此时，目标泛函的控制变量不再是分析场xa，而是分析增量δx，非线性目标泛函J(xa)的极小化问题转化为线性目标泛函J(δx)的极小化问题[7, 28]：
(7) 式(7)中，di=Hi(M0→i(xb))-yi是第i个时刻的观测增量。
显然4DVar目标泛函的式(5)和式(7)的主要差异来自于式(6)的线性近似和4DVar内外循环采用不同分辨率的插值误差。为评估TL_NMRF_CP方案在4DVar的效果，本节计算线性目标泛函J(δx)和非线性目标泛函J(xa)的相对差异
(8) 该相对差异反映式(6)中切线性算子δHiL0→i与非线性算子HiM0→i的线性近似程度，相对差异越小，说明两者的近似程度越好。
基于式(7)，利用CMA-GFS 4DVar系统同化背景场xb和观测资料得到切线性目标泛函J(δx)的结果和分析场xa；基于式(5)，利用分析场xa和观测资料得到非线性目标泛函J(xa)的结果；基于式(8)得到目标泛函的相对差异。
3.2 个例分析
与2.1节相同，本节也采用CMA-GFS V3.0版本，选择与2.3节相同的个例：2019年6月1日个例和2019年12月1日个例。试验方案如表 1所示，采用有预调节的Lanczos-CG极小化算法迭代50次[28-29]，基于式(8)，为更准确地描述TL_NMRF_CP方案和TL_MRF方案差异，4DVar试验内外循环采用相同的分辨率，以减少4DVar内外循环插值的影响。试验同化的观测资料包括探空观测的温度、风和比湿，地面观测的气压，船舶观测的气压，飞机观测的风，云导风，洋面散射计观测的风以及掩星的折射率。由于TL_NMRF_CP方案主要影响TLM模式对边界层的预报效果，未同化卫星资料。本节设计两组试验：控制试验4DVar_MRF，边界层线性化方案采用TL_MRF方案；对比试验4DVar_NMRF_CP，边界层线性化方案采用TL_NMRF_CP方案。
表 1 CMA-GFS 4DVar试验设置Table 1. Setting of CMA-GFS 4DVar test设置 详细配置 水平分辨率 外循环为1.0°×1.0°，内循环为1.0°×1.0° 模式积分步长 外循环为450 s，内循环为900 s 垂直层数 87层 同化时间窗长度 6 h 观测剖分间隔 30 m 线性化物理过程 垂直扩散、地形阻塞流拖曳、对流参数化、大尺度凝结 极小化算法 有预调节的Lanczos-CG算法 重力波控制 数字滤波弱约束 最大极小化迭代次数 50次 如图 10所示，在迭代次数相同(40次)情况下，两个个例4DVar_NMRF_CP试验的目标泛函收敛效率均高于4DVar_MRF试验，这说明TL_NMRF_CP方案可以提高4DVar极小化的收敛效率。利用式(8)计算目标泛函相对差异，可以看到TL_NMRF_CP方案可以使2019年6月1日个例4DVar目标泛函的相对差异从7.48%减少到7.01%，2019年12月1日个例4DVar目标泛函的相对差异由4.71% 减少到3.91%。这说明相较于TL_MRF方案，TL_NMRF_CP方案通过改善CMA-GFS TLM的预报精度，提高了式(6)的切线性近似，从而降低了CMA-GFS 4DVar目标泛函的相对差异。
![]()
图 10 CMA-GFS 4DVar目标泛函的收敛Figure 10. Convergence of the cost function under CMA-GFS 4DVar3.3 批量试验检验
为了检验TL_NMRF_CP方案在CMA-GFS 4DVar循环同化试验中的预报效果，本节设计两组4DVar循环同化和预报试验：控制试验TL_MRF，边界层线性化方案采用4DVar_MRF方案；对比试验4DVar _NMRF_CP，边界层线性化方案采用TL_NMRF_CP方案。试验设置如表 1所示，积分步长外循环为450 s，内循环为900 s；最大极小化迭代次数为50次;但水平分辨率外循环为0.5°×0.5°，内循环为1.5°×1.5°。循环同化日期为2019年3月1日—2019年4月30日，同化所采用资料与CMA-GFS 4DVar业务系统一致，包括各类常规和卫星观测资料(探空观测的温度、风和相对湿度，地面观测的气压、船舶观测的气压，飞机观测的风，云导风，洋面散射计观测的风，掩星折射率，NOAA卫星的辐射率，METOP卫星的辐射率，风云卫星的辐射率等)[7]。预报试验的起报时刻为12：00(世界时)，预报时效为192 h。
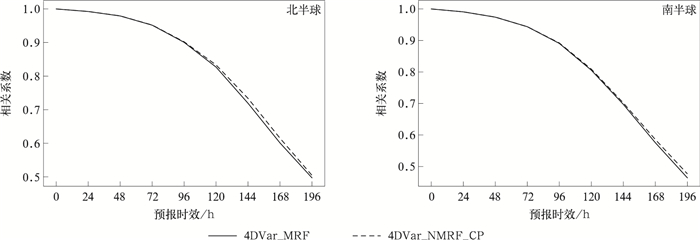
经统计，两组4DVar循环同化试验的结果差异很小，此处不详细列出。图 11是两组试验基于各自分析场计算的700 hPa位势高度相关系数。为了剔除循环同化试验受到初始时刻(2019年3月1日)背景场调整适应(spin-up)的影响，相关系数预报检验从第11日(2019年3月11日)开始。由图 11可以看到，4DVar_NMRF_CP试验的预报评分相关系数在北半球和南半球均高于4DVar_MRF试验。除了700 hPa位势高度相关系数外，4DVar_NMRF_CP试验在其他模式层以及其他评分效果上好于或不逊于4DVar_MRF试验。
![]()
图 11 北半球和南半球700 hPa位势高度的相关系数Figure 11. Anomaly correlations of 700 hPa geopotential height for the Northern Hemisphere and the Southern Hemisphere4. 结论
为了持续改善CMA-GFS 4DVar业务系统的预报效果，本文研发了基于C-P跳点的NMRF边界层线性化方案，在减少切线性模式扰动异常增长的情况下，为了更好保持边界层线性化切线性方案与非线性方案的一致性，TL_NMRF_CP方案中针对不同变量扰动采用更加精细的规约化处理方法，得到如下结论：
1) TL_NMRF_CP方案相对于TL_NMRF方案可有效改善CMA-GFS切线性模式中低层位温扰动、比湿扰动和风扰动的切线性预报精度。
2) TL_NMRF_CP方案可以降低CMA-GFS 4DVar内外循环不同分辨率导致目标泛函的相对差异，提高4DVar的收敛效率。
3) 通过CMA-GFS 4DVar循环同化预报试验进一步验证TL_NMRF_CP方案可提供更好的分析预报效果，目前已经在CMA-GFS 4DVar的业务化系统应用。
CMA-GFS切线性和伴随模式目前在业务上为CMA全球集合预报系统的奇异向量初值扰动[30]，下一步将TL_NMRF_CP方案应用于奇异向量计算模块中，改善集合预报初始扰动初值。
-
![]()
图 1 CMA-GFS切线性模式全球平均位温扰动相对误差垂直分布
Figure 1. Vertical distribution of global mean relative error of potential temperature perturbation in CMA-GFS tangent linear model
![]()
图 2 TL_MRF试验的位温扰动纬向平均绝对误差
Figure 2. Zonal mean absolute errors of potential temperature perturbation for TL_MRF test
![]()
图 3 TL_NMRF_CP试验位温扰动相对于TL_MRF试验的改善
Figure 3. Improvements in potential temperature perturbation of TL_NMRF_CP test relative to TL_MRF test
![]()
图 4 CMA-GFS切线性模式全球平均比湿扰动相对误差垂直分布
Figure 4. Vertical distribution of global mean relative error of specific humidity perturbation in CMA-GFS tangent linear model
![]()
图 5 TL_MRF试验的比湿扰动纬向平均绝对误差
Figure 5. Zonal mean absolute errors of specific humidity perturbation for TL_MRF test
![]()
图 6 TL_NMRF_CP试验比湿扰动相对于TL_MRF试验的改善
Figure 6. Improvements in specific humidity perturbation of TL_NMRF_CP test relative to TL_MRF test
![]()
图 7 CMA-GFS切线性模式全球平均纬向风扰动相对误差垂直分布
Figure 7. Vertical distribution of global mean relative error of zonal wind perturbation in CMA-GFS tangent linear model
![]()
图 8 TL_MRF试验的纬向风扰动纬向平均绝对误差
Figure 8. Mean absolute errors of zonal wind perturbation for TL_MRF test
![]()
图 9 TL_NMRF_CP试验纬向风扰动相对于TL_MRF试验的改善
Figure 9. Improvements in zonal wind perturbation of TL_NMRF_CP test relative to TL_MRF test
![]()
图 10 CMA-GFS 4DVar目标泛函的收敛
Figure 10. Convergence of the cost function under CMA-GFS 4DVar
![]()
图 11 北半球和南半球700 hPa位势高度的相关系数
Figure 11. Anomaly correlations of 700 hPa geopotential height for the Northern Hemisphere and the Southern Hemisphere
表 1 CMA-GFS 4DVar试验设置
Table 1 Setting of CMA-GFS 4DVar test
设置 详细配置 水平分辨率 外循环为1.0°×1.0°，内循环为1.0°×1.0° 模式积分步长 外循环为450 s，内循环为900 s 垂直层数 87层 同化时间窗长度 6 h 观测剖分间隔 30 m 线性化物理过程 垂直扩散、地形阻塞流拖曳、对流参数化、大尺度凝结 极小化算法 有预调节的Lanczos-CG算法 重力波控制 数字滤波弱约束 最大极小化迭代次数 50次 
下载: 导出CSV
-
[1] Bauer P, Thorpe A, Brunet G.The quiet revolution of numerical weather prediction.Nature, 2015, 525(7567):47-55. DOI: 10.1038/nature14956
[2] 沈学顺, 王建捷, 李泽椿等. 中国数值天气预报的自主创新发展. 气象学报, 2020, 78(3): 451-476. Shen X H, Wang J J, Li Z C, et al. China's independent and innovative development of numerical weather prediction. Acta Meteor Sinica, 2020, 78(3): 451-476.
[3] Rabier F, Järvinen H, Klinker E, et al. The ECMWF operational implementation of four-dimensional variational assimilation. I: Experimental results with simplified physics. Quart J Roy Meteor Soc, 2000, 126(564): 1143-1170. DOI: 10.1002/qj.49712656415
[4] Klinker E, Rabier F, Kelly G, et al. The ECMWF operational implementation of four-dimensional variational assimilation. Ⅲ: Experimental results and diagnostics with operational configuration. Quart J Roy Meteor Soc, 2000, 126(564): 1191-1215. DOI: 10.1002/qj.49712656417
[5] Gauthier P, Tanguay M, Laroche S, et al. Extension of 3DVar to 4DVar: Implementation of 4DVar at the meteorological service of Canada. Mon Wea Rev, 2010, 135(6): 2339-2354.
[6] Rawlins F, Ballard S P, Bovis K J, et al. The Met Office global four-dimensional variational data assimilation scheme. Quart J Roy Meteor Soc, 2010, 133(623): 347-362.
[7] Zhang L, Liu Y Z, Liu Y, et al. The operational global four-dimensional variational data assimilation system at the China Meteorological Administration. Quart J Roy Meteor Soc, 2019, 145(722): 1-15.
[8] Courtier P, Thépaut J N, Hollingsworth A. A strategy for operational implementation of 4DVar, using an incremental approach. Quart J Roy Meteor Soc, 1994, 120(519): 1367-1387. DOI: 10.1002/qj.49712051912
[9] Errico R M. What is an adjoint model?. Bull Amer Meteor Soc, 1997, 78(11): 2577-2592. DOI: 10.1175/1520-0477(1997)078<2577:WIAAM>2.0.CO;2
[10] 刘永柱, 张林, 金之雁. GRAPES全球切线性和伴随模式的调优. 应用气象学报, 2017, 28(1): 62-71. DOI: 10.11898/1001-7313.20170106 Liu Y Z, Zhang L, Jin Z Y. The optimization of GRAPES global tangent linear model and adjoint model. J Appl Meteor Sci, 2017, 28(1): 62-71. DOI: 10.11898/1001-7313.20170106
[11] Mahfouf J F. Influence of physical processes on the tangent-linear approximation. Tellus A, 2000, 51(2): 147-166.
[12] 龚建东, 刘永柱, 张林. 面向四维变分资料同化的NSAS积云深对流参数化方案的简化及线性化研究. 气象学报, 2019, 77(4): 595-616. https://www.cnki.com.cn/Article/CJFDTOTAL-QXXB201904001.htm Gong J D, Liu Y Z, Zhang L. A study on simplification and linearization of NSAS deep convection cumulus parameterization scheme for 4D-Var. Acta Meteor Sinica, 2019, 77(4): 595-616. https://www.cnki.com.cn/Article/CJFDTOTAL-QXXB201904001.htm
[13] 刘永柱, 龚建东, 张林等. 线性化物理过程对CMA-GFS 4DVar同化的影响. 气象学报, 2019, 77(2): 196-209. https://www.cnki.com.cn/Article/CJFDTOTAL-QXXB201902003.htm Liu Y Z, Gong J D, Zhang L, et al. Influence of linearized physical processes on the CMA-GFS 4DVar. Acta Meteor Sinica, 2019, 77(2): 196-209. https://www.cnki.com.cn/Article/CJFDTOTAL-QXXB201902003.htm
[14] Zou X. Tangent linear and adjoint of "on-off" processes and their feasibility for use in 4-dimensional variational data assimilation. Tellus A, 1997, 49(1): 3-31. DOI: 10.3402/tellusa.v49i1.12209
[15] Holdaway D, Errico R. Using jacobian sensitivities to assess a linearization of the relaxed arakawa-schubert convection scheme. Quart J Roy Meteor Soc, 2014, 40(681): 1319-1332.
[16] 沈学顺, 苏勇, 胡江林, 等. GRAPES_GFS全球中期预报系统的研发和业务化. 应用气象学报, 2017, 28(1): 1-10. DOI: 10.11898/1001-7313.20170101 Shen X S, Su Y, Hu J L, et al. Development and operation transformation of GRAPES global middle-range forecast system. J Appl Meteor Sci, 2017, 28(1): 1-10. DOI: 10.11898/1001-7313.20170101
[17] 王金成, 陆慧娟, 韩威, 等. GRAPES全球三维变分同化业务系统性能. 应用气象学报, 2017, 28(1): 11-24. DOI: 10.11898/1001-7313.20170102 Wang J C, Lu H J, Han W, et al. Improvements and performances of the operational GRAPES_GFS 3Dvar system. J Appl Meteor Sci, 2017, 28(1): 11-24. DOI: 10.11898/1001-7313.20170102
[18] 黄丽萍, 邓莲堂, 王瑞春, 等. CMA-MESO关键技术集成及应用. 应用气象学报, 2022, 33(6): 641-654. DOI: 10.11898/1001-7313.20220601 Huang L P, Deng L T, Wang R C, et al. Key technologies of CMA-MESO and application to operational forecast. J Appl Meteor Sci, 2022, 33(6): 641-654. DOI: 10.11898/1001-7313.20220601
[19] 李喆, 陈炯, 马占山, 等. CMA-GFS云预报的偏差分布特征. 应用气象学报, 2022, 33(5): 527-540. DOI: 10.11898/1001-7313.20220502 Li Z, Chen J, Ma Z S, et al. Deviation distribution features of CMA-GFS cloud prediction. J Appl Meteor Sci, 2022, 33(5): 527-540. DOI: 10.11898/1001-7313.20220502
[20] Charney J G, Phillips N A. Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows. J Atmos Sci, 1953, 10(2): 71-99.
[21] Han J, Pan H L. Revision of convection and vertical diffusion schemes in the NCEP global forecast system. Wea Forecasting, 2010, 26: 520-533.
[22] Lorenz E N. Energy and numerical weather prediction. Tellus, 1960, 12: 364-373.
[23] Chen J, Ma Z, Li Z, et al. Vertical diffusion and cloud scheme coupling to the Charney-Phillips vertical grid in CMA-GFS global forecast system. Quart J Roy Meteor Soc, 2020, 146(730): 2191-2204.
[24] 陈炯, 马占山, 苏勇. 适用于CMA-GFS模式C-P边界层方案的设计和实现. 应用气象学报, 2017, 28(1): 52-61. DOI: 10.11898/1001-7313.20170105 Chen J, Ma Z S, Su Y. Boundary layer coupling to Charney-Phillips vertical grid in CMA-GFS Model. J Appl Meteor Sci, 2017, 28(1): 52-61. DOI: 10.11898/1001-7313.20170105
[25] 张萌, 于海鹏, 黄建平, 等. GRAPES_GFS 2.0模式非系统误差评估. 应用气象学报, 2019, 30(3): 332-344. DOI: 10.11898/1001-7313.20190307 Zhang M, Yu H P, Huang J P, et al. Assessment on unsystematic errors of GRAPES_GFS 2.0. J Appl Meteor Sci, 2019, 30(3): 332-344. DOI: 10.11898/1001-7313.20190307
[26] Hong S Y, Pan H L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon Wea Rev, 1996, 124(10): 2322-2339.
[27] 张林, 朱宗申. GRAPES模式切线性垂直扩散方案的误差分析和改进. 应用气象学报, 2008, 19(2): 194-200. http://qikan.camscma.cn/article/id/20080235 Zhang L, Zhu Z S. Estimation of linearized vertical diffusion scheme in GRAPES model. J Appl Meteor Sci, 2008, 19(2): 194-200. http://qikan.camscma.cn/article/id/20080235
[28] Liu Y Z, Zhang L, Lian Z H. Conjugate gradient algorithm in the four-dimensional variational data assimilation system in CMA-GFS. J Meteor Res, 2018, 32(6): 974-984.
[29] 张林, 刘永柱. GRAPES全球四维变分同化系统极小化算法预调节. 应用气象学报, 2017, 28(2): 168-176. DOI: 10.11898/1001-7313.20170204 Zhang L, Liu Y Z. The preconditioning of minimization algorithm in GRAPES global four-dimensional variational data assimilation system. J Appl Meteor Sci, 2017, 28(2): 168-176. DOI: 10.11898/1001-7313.20170204
[30] 霍振华, 李晓莉, 陈静, 等. 基于背景场奇异向量的CMA全球集合预报试验. 应用气象学报, 2022, 33(6): 655-667. DOI: 10.11898/1001-7313.20220602 Huo Z H, Li X L, Chen J, et al. CMA global ensemble prediction using singular vectors from background field. J Appl Meteor Sci, 2022, 33(6): 655-667. DOI: 10.11898/1001-7313.20220602
-
期刊类型引用(6)
1. 邓莲堂，朱立娟，张进，于翡. CMA-MESO 3 km模式中自适应时间步长方案试验. 气象科技. 2025(01): 10-21 . 
百度学术
2. 王凡，龚建东，王瑞春，陈耀登. CMA全球混合四维变分同化系统的方法研究. 气象学报. 2024(05): 709-720 . 百度学术
3. 陈良吕，夏宇. 对流尺度集合预报成员数对降水预报的影响. 应用气象学报. 2023(02): 142-153 . 本站查看
4. 常煜，温建伟，杨雪峰，高绍鑫，于溥天. 基于CMA-TYM和SCMOC的嫩江流域暴雨检验. 应用气象学报. 2023(02): 154-165 . 本站查看
5. 王海平. 高空冷涡对台风烟花(2106)路径的影响. 应用气象学报. 2023(05): 586-597 . 本站查看
6. 张进，孙健，沈学顺，苏勇，马占山，井浩，刘奇俊，张红亮，蒋沁谷，陈峰峰，李喆，金之雁，伍湘君，梁妙玲，刘琨. CMA-GFS V4.0模式关键技术研发和业务化. 应用气象学报. 2023(05): 513-526 . 本站查看
其他类型引用(2)
计量
- 文章访问数: 1305
- HTML全文浏览量: 306
- PDF下载量: 97
- 被引次数: 8
