一种在异构系统中实现负载平衡的方法
AN ALGORITHMFOR LOAD BALANCING IN A HETEROGENEOUS SYSTEM
-
摘要: 提出了在异构系统实现负载平衡的区域分解算法和实现负载平衡的计算方法,利用它的负反馈性质解决了异构系统处理机计算速度测量误差造成的负载测量不准问题,并对处理机速度变化,速度测量误差、处理机数量、网格点计算量的分布等因素的影响进行了计算,结果表明本方法具有很强的平衡负载能力和较强的适应性;根据计算结果提出了解决模式网格点计算量不易测量问题的解决方案,并用扩散方程和模拟物理过程进行试验,试验表明这种方法是可行的,平衡负载的效果十分显著。Abstract: Load balancing is a crucial problem in a heterogeneous system such as PC or workstation clusters, which has been widely used in the research and development of numerical weather prediction. A load balancing algorithm, based on feedback, is presented to eliminate the influence of uncertainty of processor speed, which is difficult to measure precisely. The influences of variation of processor speed, load distribution, errors of tested processor speed, etc., have been calculated. The results show that this method is quite robust. The diffusion equation and the simulated physical processes are used to test the algorithm, which shows that it is feasible and can balance the load quite weill.
-
引言
分布式并行处理技术已被越来越多的人所接受,机群系统以其低廉的价格和优异的性能得到众多用户的青睐,无论在国内还是国外,将机群系统用于数值预报研究、开发的单位越来越多,有的甚至用于日常数值预报业务,取得了很好的效果。但是分布式并行处理实现负载平衡比共享并行困难得多。目前很多数值预报模式,如MM5[1],WRF[2],德国的GME模式[3]都未涉及该问题[4],这在很大程度上限制了模式的并行规模和应用范围。
负载平衡可以分为动态与静态两种,如果在运行之前可以预知模式的计算负载分布情况,负载的划分是静态负载平衡问题。反之,需要在模式运行时监测负载情况并根据监测信息动态调整模式负载的划分,是动态负载平衡问题。数值预报的负载不平衡来源于多个方面,如积云对流参数化和云微物理过程等,这些都是随天气情况变化的计算负载。另一个可能的负载不平衡来源是计算机。由于采用机群系统的用户越来越多,很多用户需要用不同型号的微机或工作站和高速互联网组成机群系统。如果并行系统中每个结点是相同的,称为同构系统,反之称为异构系统。采用异构系统的数值预报模式必须有相应的负载平衡措施,否则,模式运算速度取决于系统中最慢的处理机的运算速度。由于异构系统的构成变化很大,每个节点的计算速度不易测量,造成计算量估算不准,影响负载平衡的实现。本文提出了一种负载平衡方法,它具有负反馈性质,可以在对计算量估算不准的情况下平衡负载,解决数值预报模式的静态和动态负载平衡问题。
1. 区域分解算法
首先我们定义负载平衡函数,设P个处理机完成一个时间步的时间为Tl,l=0,1 …,P-1。定义:

其中Tav为各处理机平均计算时间,Tmax为各处理机中最大的计算时间,也就是并行处理时间。负载平衡函数为:

(1) 显然,I为零时负载达到平衡,大于零表示负载不平衡。
区域分解是实现分布式并行处理的基础,作者曾提出在同构环境中的区域划分方法[5],本文将该方法扩展到异构系统中。定义预报区域G是矩形区域,东西、南北方向的网格点数各为Nx、Ny。格点 (i,j) 的计算负载为wij,负载总和为






其中Mod (P,N) 是P被N除的余数,





首先按以下方法将区域G划分成N个区域:
令k=1
对j从Ny至1增量为-1循环开始
对i从1至Nx循环开始
将 (i,j) 点标为k
计算Σwij,如果

对i循环结束
对j循环结束
将N个区域的所有格点按照内循环i由小至大,中循环j由小至大,外循环是区域k,由1至N的顺序排列成一维数组,即将所有格点从1至N区排列,区内按照i从小至大,j从小至大的顺序排列成一维数组,设下标为l。按照以下方法将G划分成P个子区域:
令SUM=0
令k=1
对l从1至Nx·Ny循环
格点l标记为k
令SUM=SUM +wl
如果

对l循环结束
设G内第k子区域的计算负载为


其中,w max=max (wij),(i,j)∈G,所以对任意两个子区域有

由于该方法允许将行或列断开使得子区域的形状出现小台阶,每一个台阶会增加一个格点的通信量,最多会增加P-1个格点的通信量。所以,通信的增加量是很少的。
2. 实现负载平衡的负反馈方法
如果可以精确测定每个处理机的处理速度和每个格点的计算负载,上述方法就可以近似达到负载平衡,但是测定处理机的计算速度本身就是一个复杂的问题,它与处理机硬件、编译器、编程、内存的使用等很多因素相关。其次,每个网格点的计算量的测定也是与处理机硬件、编译器、编程的优化程度等因素有关,精确测定每个网格点的计算量是不现实,甚至是不可能的。因此必须研究在不能精确测定处理机计算速度和每个网格点的计算负载条件下实现负载平衡的方法。
本文提出的方法如下:
步骤1:利用一个速度估算子程序估算处理机的计算速度。该子程序只是进行一些计算,这些计算应能代表模式的计算特点,如加、减、乘、除、指数运算等,测出该子程序的计算时间T′l,令

步骤2:假定每个网格点的计算量为w′ij=1。
步骤3:按照第一节的方法,对网格点进行分区。并将数据按照分区进行分配。
步骤4:进行一个时间步长的计算,在计算过程中,测出每个网格点的计算时间tij和每个处理机的总计算时间Tl
步骤5:根据式 (1) 计算负载平衡函数I
步骤6:如果I小于阈值ξ,则保持现有的分区,跳到步骤4进行下一个时间步长的计算; 如果I大于阈值ξ,令w′ij=s′lt ij,其中l为格点i,j所在的处理机编号。跳到步骤3重新进行分区。重复上述过程直至结束。
该方法可以在不精确测定处理机计算速度的情况下,利用它的负反馈性质逐渐逼近负载平衡。具体过程是,如果s′l大于真实计算速度,分配在处理机l上的计算负载会多一些,在第2次对格点的计算负载进行估算时,由于tij是实测值,所以w′ij=s′lt ij,就会比实际计算负载大一些,如果第2次循环时区域划分变化不大,分配在该处理机上的部分网格点就会移到其它处理机上,降低该处理机的总计算负载。可以看出,该方法不能精确测定处理机计算速度和网格点的计算负载。其负反馈机制是通过调整每个网格点的“计算负载”实现的,很显然,这种负反馈机制只有在区域划分变化不大,多数网格点仍然处于同一个处理机的情况下才有作用。如果s′l与实际相差太大,就会使同一个网格点的计算量w′ij=s′ltij在不同处理机上差别很大,循环的收敛速度就会很慢,甚至不收敛。
3. 负载平衡方法试验
为了考察该方法平衡负载的能力,我们设计了针对数值预报的并行处理的试验。设预报区域的网格点数量Nx×Ny为320 ×160,在区域中部,有半径为10个格距的区域计算负载是周围其它格点的c倍,即

用来模拟格点之间负载不均匀的情况。分别用32、64、128、256个处理机进行试验。假定处理机速度为:

其中,random (r) 为0~r之间的随机数。这样,最快与最慢处理速度之比约为r:1,“测定”的处理机速度为:

其中rand (a) 是 (-a,a) 之间的随机数,a分别取为10 %、20 %、30 %,相当于测量误差。试验方法如下:
步骤1:用随机数发生器计算出处理机的“实际”计算速度sl和“测量”计算速度s′l
步骤2:令w′ij=1,用s′l、w′ij和第1节介绍的方法进行区域划分,并令m=0。
步骤3:每个格点的计算时间用w′ij和sl求出,令

步骤4:将每个区域的wij求和并除以sl,求出每个处理机的计算时间Tl,用式 (1) 计算负载平衡函数I,如果I>ξ,跳到步骤3,反之结束,考察m的值。
为了减少试验偶然性的影响,重复上述试验100次,m取100次试验中的最大值。
我们分别取ξ=5 %,a=0.1、0.2、0.3,r=2.0、4.0、6.0、8.0,c=2、4、8,P=16,32,64,128,256进行试验,表 1是试验得到的m的值。
表 1 测定每个网格点计算时间条件下,P取为16,32,64,128,256达到负载平衡的循环次数m
由表 1可以看出,在处理机数量不多的情况下,处理机速度的误差影响并不大,对于处理机数量较多时,应尽量将处理机速度测量准确。系统内处理机速度相差越大,循环次数越多,尤其是在处理机数量比较多的时候,所以淘汰一些处理速度过慢的节点有利于提高平衡负载的速度。格点间计算量相差越大,实现负载平衡越困难。但在绝大多数情况下,循环2~3次均可实现负载的均衡。只有个别情况下循环次数多一些或者不能在30次内达到负载平衡函数小于5 %。所以本方法平衡负载的效果是比较好的。
在上述方法中我们假定可以测量每个网格点的计算时间,但有时测量每个网格点的计算时间是很难的,因此,我们还试验了在不能测量每个网格点的计算时间时的处理方法。我们用每个处理机上每个网格点的平均处理时间来替代每个网格点的计算时间。具体方法是将步骤3改为:将各处理机上的网格点的wij求和并算出每个处理机上的网格点数量Nl,令

可以看出,如果网格点的计算量相差在一倍左右时 (c=2),两种方法的速度差不多,如果网格点计算量相差在4倍,平均负载与实际负载相差很大,收敛速度就会很慢,若相差8倍以上基本不收敛。
在数值预报模式中,动力框架部分的计算负载是比较均匀的,但是测定每一个网格点的计算量比较困难,可以用平均网格点计算量,即便有些误差 (一般误差很少能超出1倍) 影响也不大。对于物理过程部分,网格点之间负载相差可以很大,但测定每个网格点的计算时间却比较方便。模式中可将两种方法结合使用。
表 2 不能测定每个网格点计算时间条件下,P取为16,32,64,128,256达到负载平衡的循环次数m
4. 动态负载平衡试验
数值天气预报的计算负载是随计算过程而变化的,需要在计算过程中,根据测定计算负载的分布情况动态地调整每个节点的计算量,是一种动态的负载平衡过程。根据R.W.Ford[6]的研究,数值预报模式中每个网格点的计算量随时间积分过程是一个缓慢的变化过程,上一个时间步与下一个时间步的计算时间相差不大。所以,调整一次负载,可在一段时间内起作用。很显然,如果可在1个循环步内将负载调整好,本方法也可用对负载进行动态调整。对于需要多个时间步循环才能实现负载平衡,同时负载还在变化,效果就比较差了。
数值预报程序量庞大,直接试验困难比较大。因此,我们利用一个简化的模型进行试验。数值预报计算主要集中在动力部分和物理过程部分。随着模式的细化,物理过程的计算量越来越大,可以达到动力部分的几倍到十几倍,且分辨率越高,所占比重越大。它也是负载不平衡的主要来源。
二阶线性扩散方程虽只是数值预报模式的一小部分,但是它与模式动力过程的计算特点以及数据通信方式是一样的,因此用它模拟模式动力过程部分的计算可以说明问题,其方程是:

离散化形式为:

其中F是扩散变量,Kx,Ky,Kz分别是x,y,z三方向上的扩散系数,Δt,Δx,Δy,Δz是时间步长和三个方向上的格距。离散化后的网格点是 (Nx,Ny,Nz) 阶三维矩阵,取固定边条件。
物理过程每个格点的计算彼此相互独立,计算量由该点的天气、地理、时间等因素决定。我们采用在格点 (i,j) 上计算sin和cos函数Zij次来模拟物理过程。Zij定义为:

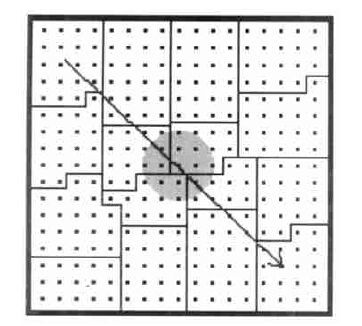
(14) 表示在格点 (i,j) 上要计算Zij次sin和cos函数。其中 (ic,jc) 是“天气系统”的中心,该中心以20个时间步一个格距的速度自西北向东南方向移动,预报区域是101 ×101的正方形区域,垂直层次有100层 (图 1)。
计算过程如下:
假定每个网格点的计算相同,计算分区并将数据分布到每个处理机上;
时间积分循环开始:
每个处理机从周围处理机上取得所需要的数据;
每个处理机在相应的区域内进行本时间步的计算并对每个网格的计算时间计时,对本处理机的总计算时间计时; 计算负载平衡函数;
如果负载平衡函数连续大于给定阈值5次,则根据测得的每个网格点的计算量重新计算分区并按照新的分区将数据重分布。
时间积分循环结束。
试验研究在IBM的SP计算机上进行,它有两种类型的结点,POWER3和POWERPC,在试验中,我们使用了两个POWER3节点和两个POWER PC节点。在试验中我们发现,系统有时会出现随机扰动,对负载平衡影响很大。我们用连续大于给定阈值5次作为触发数据重分布的条件以避免随机扰动的影响。试验中我们取阈值为0.1并与不进行数据重分布进行对比。图 2是试验结果。可以看出,采用了动态负载平衡的效果比未采用该技术的效果要好得多。通过几次调整,负载平衡函数维持在比较低的水平; 阈值的选取对调整的次数有很大影响,较小的阈值虽然可以使负载更加平衡,但是调整次数过多本身也会有很大的开销。应选取适合的阈值。
5. 结论
本文设计了一种在异构系统中实现负载平衡的区域分解算法,并提出了在不能精确测定处理机计算速度时实现负载平衡的方法,并针对处理机速度高低分布、处理机速度误差、处理机数量、网格点计算量分布、网格点计算量确定方法等因素的影响进行计算,结果表明本方法具有很强的平衡负载能力和较强的适应性,在处理机速度对比,网格点计算量对比、处理机速度误差都比较大的情况下仍然可以比较好地平衡负载; 在网格点计算量比较均匀 (格点计算量相差约1倍) 的情况下,可以用平均计算量代替网格点计算量,但是如果计算量相差比较悬殊,就不能用平均网格点计算量替代; 提出了针对数值模式动力框架和物理过程计算量分布的不同特点将二者结合的方式解决模式网格点计算量的测量问题的方法,并用扩散方程和模拟物理过程进行试验,试验表明这种方法是可行的,平衡负载的效果十分显著。
-
表 1 测定每个网格点计算时间条件下,P取为16,32,64,128,256达到负载平衡的循环次数m

表 2 不能测定每个网格点计算时间条件下,P取为16,32,64,128,256达到负载平衡的循环次数m

-
Michalakes J, Canfield T, Nanjundiah R, et al. Parallel implementation, validation and performance of MM5, coming of age. Proceedings of the Sixth ECMWF Workshop on the Use of Parallel Processors in Meteorology. World Scientific, River Edge, New Jersey, 1995. 266-276. http://www.gbv.de/dms/tib-ub-hannover/198050437.pdf
Michalakes J, Dudhia J, Gill D, et al. Design of a next-generation regional weather research and forecast model, towards teracomputing. Proceedings of the Eighth ECMWF Workshop on the Use of Parallel Processors in Meteorology. World Scientific, River Edge, New Jersey, 1999. 117-123.
Schattler U. Model development for parallel computers at DWD, making its mark. Proceedings of the Seventh ECMWF Workshop on the Use of parallel Processors in Meteorology. World Scientific, River Edge, New Jersey, 1997. 83-99. http://www.gbv.de/dms/tib-ub-hannover/249689324.pdf
舒继武, 郑纬民, 沈美明, 等, 大规模问题数据并行性能的分析.软件学报, 2000, 11(5):628-633. http://www.cnki.com.cn/Article/CJFDTOTAL-RJXB200005007.htm Ford R W, Burton P M. Load balancing physics routines, towards teracomputing. Proceedings of the Eighth ECMWF Workshop on the Use of parallel Processors in Meteorology. World Scientific, River Edge, New Jersey, 1999. 147-159. http://www.worldcat.org/oclc/43250502
金之雁, 王鼎兴.一种有限差分格式负载平衡区域分解方法.气象学报, 2002, 60(2):188-193.

 设为首页
设为首页 加入收藏
加入收藏


 下载:
下载: