对偶Kriging插值方法在气象资料分析中的应用
The Application of Dual Kriging Interpolating Method to Meteorological Data Analysis
-
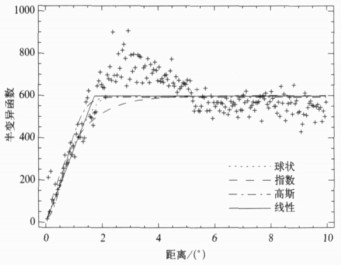
摘要: 非对偶Kriging方法是一种局部插值, 因此对每个插值点都要重新求解Kriging线性系统从而非常耗时。该文介绍了通过等价变换将泛Kriging方法转换成对偶Kriging方法, 对偶Kriging方法是一种全局插值, 其Kriging线性系统不依赖插值点, 因此仅需一次求解Kriging线性系统即可计算所有插值点的值, 从而极大提高了计算效率。数值试验的实际计算表明, 对偶Kriging方法不仅计算精度完全与泛Kriging方法一致, 整体效果相当于或优于GrADS绘图软件的Cressman方法; 而且对偶Kriging方法的计算效率远高于泛Kriging方法。最后, 该文通过统计与拟合得到了降水的4类半变异函数模型的表达式, 并通过敏感试验研究4类半变异函数模型对降水分析精度的影响。
-
关键词:
- 对偶Kriging;
- Kriging线性系统;
- 等价变换;
- 计算效率;
- 半变异函数
Abstract: Kriging method is an interpolating method based on the spatial statistical correlation of the samples. The core idea implicated in Kriging method is that each sample is assigned with different weight according to the spatial correlation among the sample points, and the estimated error is minimized. So, it can be summarized to be the best linear unbiased estimator of a random function. Non-dual Kriging method is a local interpolator for the interpolation at each node and the solution of a new Kriging linear system is required by which the location of interpolating node is explicitly depended on. Therefore, non-dual Kriging method is quite time consuming for the solution of a new Kriging linear system for every interpolating point. By equivalent transform, the Universal Kriging method can be transformed to Dual Kriging method, which is a global interpolator for its Kriging linear system is independent of the interpolating point. Therefore, the Kriging linear system is solved by the Dual Kriging method only once to interpolate all points, so the computational efficiency is significantly improved and is of great value in meteorology and oceanography where large data sets are to be interpolated. Furthermore, the result of the numerical experiment shows that Dual Kriging method is not only equivalent to Universal Kriging method in accuracy and comparable to or superior to the Cressman method built in GrADS, but also far superior to Universal Kriging method in computational efficiency. In order to improve the accuracy, efficiency and flexibility of Dual Kriging method, several unique techniques are adopted in the implementation of the computational scheme:the solution of Dual Kriging linear system using partial pivoting LU decomposition and iterative improvement, the fitting of the trend by SVD linear fitting method, Levenberg-Marquatdt iterative method for the non-linear parameters fitting of the semivariance model, and the flexible parameter configuration by the FORTRAN 90 modular interface. Finally, four kinds of semivariance expressions are obtained by fitting the statistical sample semivariance derived from the statistics of summer precipitation in the Eastern and Southern China, and the sensitivity of these four kinds of semivariance models to the accuracy of precipitation interpolation is analyzed using the Dual Kriging method. It is found that exponential semivariance model is resulted in the best analysis, spherical semivarance model is better, Gaussian and linear semivariance is the worst. It is reasonable since the exponential semivariance model is the smoothest and its range is the longest, then the interpolation is made more accurate by the smooth weight contributions from more samples around the interpolating point. Therefore, the longer the range is, the more smooth the semivariance varies, the more accurately the precipitation within the isotropic range is interpolated by the Dual Kriging method. In summary, the Dual Kriging method is superior to non-dual Kriging method and Cressman method, and as an efficient and accurate best linear unbiased interpolator, more applications in meteorology and oceanography will be gained. -
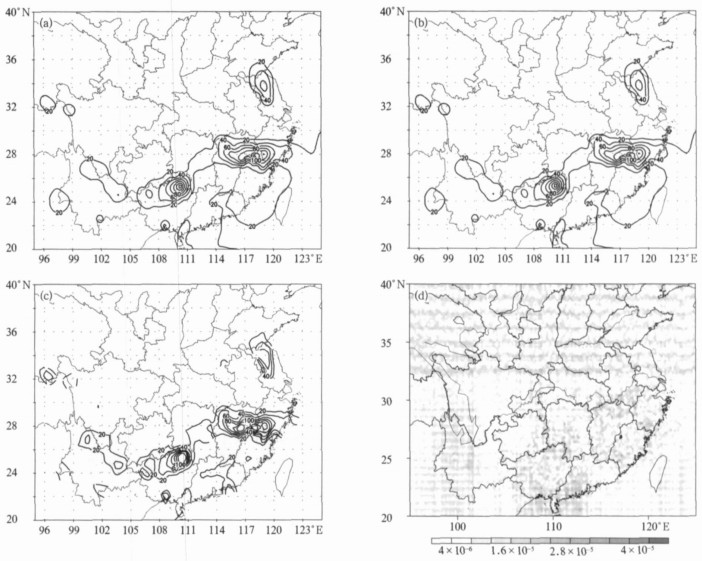
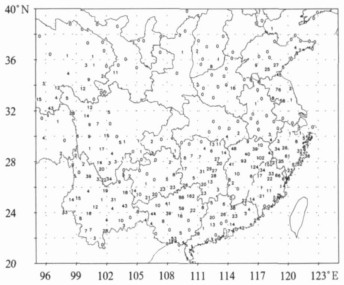
图 2 3种方法分析的降水量等值线以及对偶Kriging方法与泛Kriging方法差异 (单位:mm)
(a) 对偶Kriging方法, (b) 泛Kriging方法, (c) Cressman方法, (d) 对偶Kriging方法与泛Kriging方法之差
Fig. 2 The precipitation contours by these three methods and the difference of the contour by Dual Kriging to that by Universal Kriging (unit:mm)
(a) Dual Kriging method, (b) Universal Kriging method, (c) Cressman method, (d) the difference
表 1 倾向项d(X) 与向量X的维数和pk(X) 多项式的最高次数的关系
Table 1 The relationship between the trend d(X) and the dimension of vector X, the order of polynomial pk(X)

表 2 3种方法的最大值、最小值与实况对比
Table 2 The comparison among these three methods by comparing their max/min value with observations

表 3 对偶Kriging与泛Kriging的计算效率对比
Table 3 The comparision of the efficiency between Dual Kriging method and Universal Kriging method

表 4 4类半变异函数模型对对偶Kriging插值精度的影响
Table 4 The impact of four kinds of semivariance on the precision of Dual Kriging method

-
[1] 常文渊, 戴新刚, 陈洪武.地质统计学在气象要素场插值的实例研究.地球物理学报, 2004, 47(6):982-990. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200406007.htm [2] 张玉玲, 吴辉碇, 王晓林.数值天气预报.北京:科学出版社, 1986:382-384. [3] 曾忠一.气象与遥测资料的客观分析.台北:中央研究院物理研究所, 1987:93-97. [4] 洪玉振.克里格统计理论研究新解.河海科技进展, 1994, 14 (4):31-34. http://www.cnki.com.cn/Article/CJFDTOTAL-SLSD199404007.htm [5] Matheron G. Principles of geostatistics.Economic Geology, 1963, 58(8):1246-1266. doi: 10.2113/gsecongeo.58.8.1246 [6] Chiles J P, Delfiner P.Geostatistics:Modeling Spatial Uncertainty. New York:John Wiley & Sons, 1999. [7] Christakos G. Modern Spatiotemporal Geostatistics. New York:Oxford University Press, 2000. [8] Cressie N. Statistics for Spatial Data. New York:John Wiley & Sons, 1993. [9] Ripley B D.Spatial Statistics. New York:John Wiley & Sons, 1981. [10] 岳文泽, 徐建华, 徐丽华.基于地统计方法的气候要素空间插值研究.高原气象, 2005, 24(6):974-980. http://www.cnki.com.cn/Article/CJFDTOTAL-GYQX200506017.htm [11] 刘峰.应用Kriging算法实现气象资料空间内插.气象科技, 2004, 32(2):110-115. http://www.cnki.com.cn/Article/CJFDTOTAL-QXKJ200402009.htm [12] Le Roux D Y, Lin C A, Staniforth A. An accurate interpolating scheme for semi-Lagrangian advection on an unstructured mesh for ocean modeling.Tellus, 49(1):119-138. https://www.researchgate.net/publication/227780439_An_accurate_interpolating_scheme_for_semi-Lagrangian_advection_on_an_unstructured_mesh_for_ocean_modelling [13] William H P, Teukolsky S A, William T V, et al.Numerical Recipes in C++, Second Edition. Beijing:Publishing House of Electronics Industry, 2003:46-59; 661-704. [14] 魏凤英.气候统计诊断与预测方法研究进展.应用气象学报, 2006, 17(6):736-742. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200606122&flag=1 [15] 《现代应用数学手册》编委会.现代应用数学手册:计算与数值分析卷.北京:清华大学出版社, 2005:399-421. -

 设为首页
设为首页 加入收藏
加入收藏


 下载:
下载: