动力季节预测中预报误差与物理因子的关系
Relationships Between Prediction Errors and Physical Predictors in Dynamical Seasonal Prediction
-
摘要: 为了在动力季节预测中更好地运用统计经验来改进预报, 从研究气候系统物理因子影响模式预报误差的角度入手, 探讨了与气候模式有关的统计经验获取问题, 并利用国家气候中心海-气耦合模式的历史回报数据, 考察了动力季节预测中夏季环流和降水的预报误差与主要物理因子, 包括Niño3区海温指数、太平洋年代际振荡指数、南北半球环状模指数以及北大西洋涛动指数相关关系。分析结果显示:上述物理因子与模式预报的夏季环流和降水误差之间存在前期或同期的某种显著相关关系, 并且显著关系分布随因子的不同而表现出明显不同的区域性特征, 这为发展一种基于预报因子的误差订正新方法提供了新思路。Abstract: In order to better improve dynamical seasonal prediction by utilizing statistical experiences, the problem of capturing statistical experiences associated with climate model is discussed from the point of view of studying the impacts of physical predictors in climate system on model prediction errors. As model errors objectively exist in climate model and vary with the sate of climate system, the prediction errors of model change with state. Thus, deeply examining the characteristics that how the prediction errors of model are influenced by climate system state has important values to capture the statistical experiences associated with model and improve dynamical prediction in terms of the combination of dynamical and statistical methods. Problems and their meanings related with above characteristics are primarily proposed.Based on hindcast data of air-ocean coupled general circulation model in National Climate Center, China Meteorological Administration, the relationship between the prediction errors of summer mean circulation and total precipitation in dynamical seasonal prediction, and some primary physical predictors are comprehensively examined. These physical predictors selected include the sea surface temperature index in Niño3 region, the Pacific decadal oscillation index, the southern hemispheric annular mode index, the northern hemispheric annular mode index, and the North Atlantic oscillation index, which reflects the prevailing modes of interannual variability in climate system over tropics and extratropics.Results of correlation analyses show that there are some significant early or simultaneous relationships between the above-mentioned physical predictors and the model prediction errors of summer circulation and precipitation. In the five selected physical predictors, the sea surface temperature index in Niño3 region mainly correlates with the prediction errors of low-latitude circulation and precipitation. The correlationship between the Pacific decadal oscillation index and prediction errors is mostly characterized by simultaneous correlations and is significant not only over some low-latitude but also mid-and high-latitude areas. The southern and northern hemispheric annular mode indices standing for the leading modes over two extratropics are not corresponding to the evident early correlation with only some significant correlations over partial extratropics, whereas the simultaneous correlations are relatively evident and characterized by the distribution patterns similar to spatial modes of the two extratropical indices. The correlation situations between the North Atlantic oscillation index and circulation errors are very analogical to those corresponding to the northern hemispheric annular mode index, whereas the early and simultaneous correlations between it and precipitation errors are much better than those corresponding to circulation errors.By examining the physical processes that physical predictor influences the distribution of model prediction errors, investigating the relationship between predictor and prediction errors will not only help to evaluate the performance of model and provide reference for improving model, but also benefit the development of the new prediction strategy and methodology for correcting prediction errors. Thereby, physical basis and practical reference are provided to develop new method of predictor-based error correction, which will be studied and verified in further work.
-
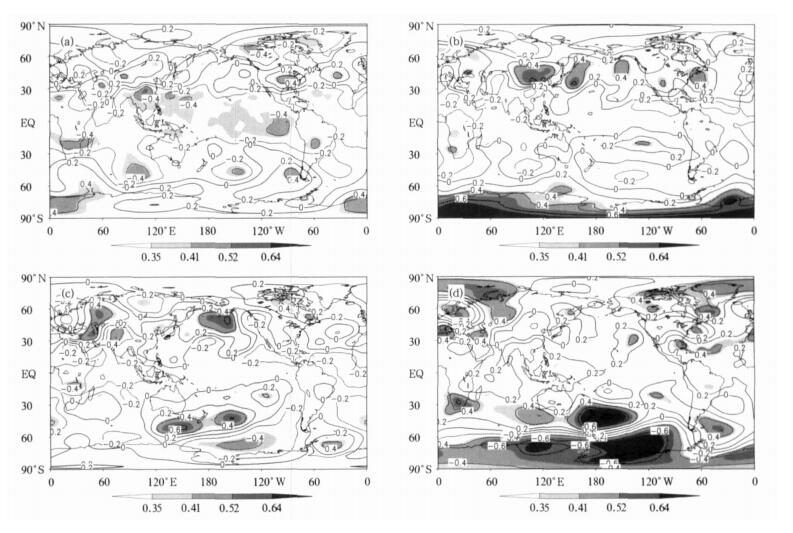
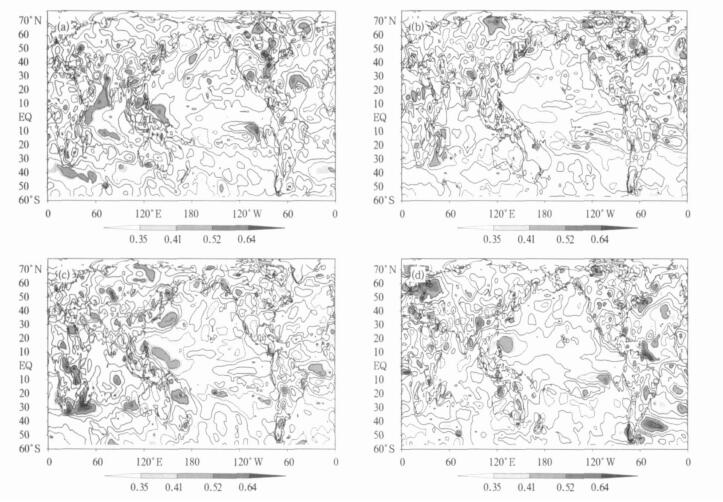
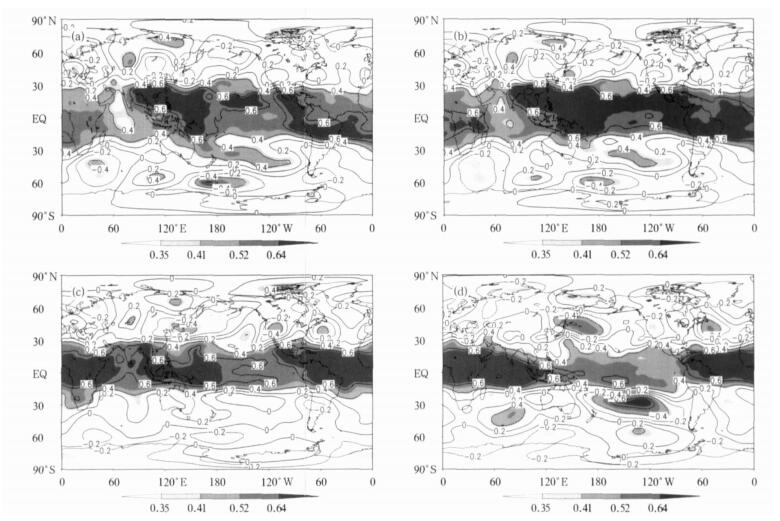
图 1 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的Niño3区海温指数与夏季500 hPa高度预报误差相关分析
(阴影层次的相关系数0.35, 0.41, 0.52和0.64, 分别对应着0.1, 0.05, 0.01, 0.001的t检验显著性水平, 下同)
Fig. 1 TCCs between the prediction errors of summer mean 500 hPa geopotential height and the early autumn (a), winter (b), spring (c) and simultaneous summer (d) NINO3Is respectively
(where numbers 0.35, 0.41, 0.52 and 0.64 stand for levels of 0.1, 0.05, 0.01, 0.001 based on Student's t-test, respectively)
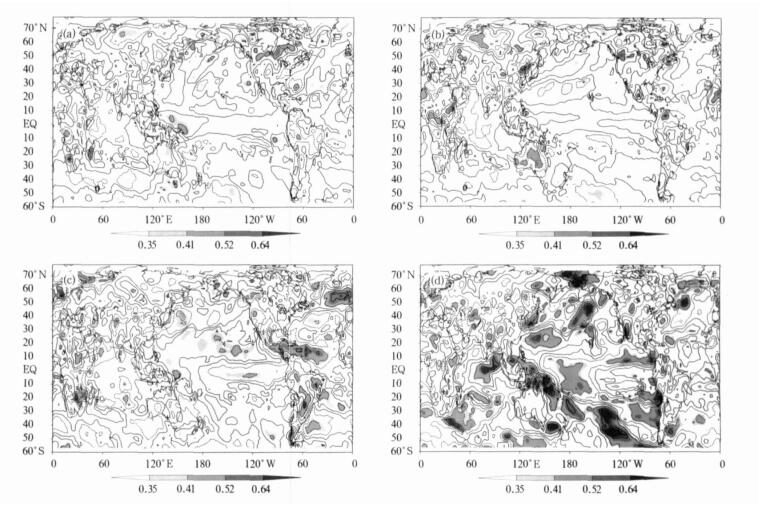
图 2 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 太平洋年代际振荡指数与夏季500 hPa高度预报误差相关分析
Fig. 2 Same as in Fig.1, but for the Pacific decadal oscillation index
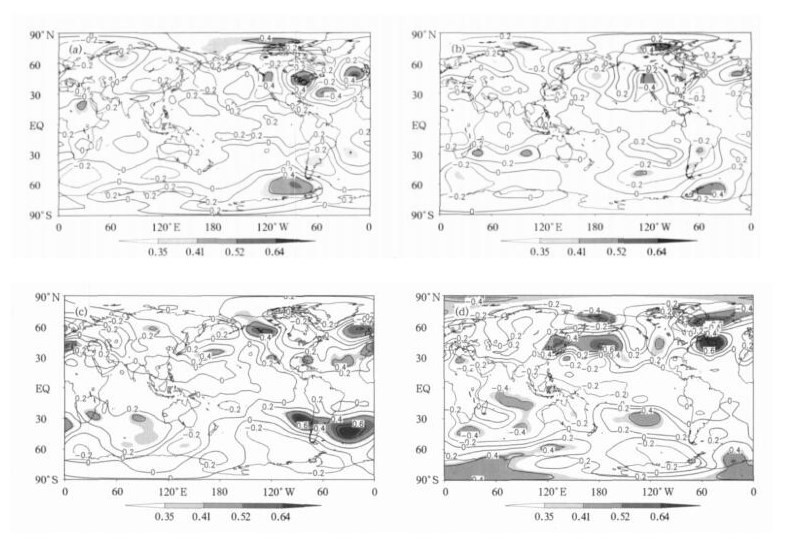
图 3 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的南半球环状模指数与夏季500 hPa高度预报误差相关分析
Fig. 3 Same as in Fig.1, but for the Southern Hemispheric annular mode index
图 4 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的南半球环状模指数与夏季500 hPa高度预报误差相关分析
Fig. 4 Same as in Fig.1, but for the Southern Hemispheric annular mode index
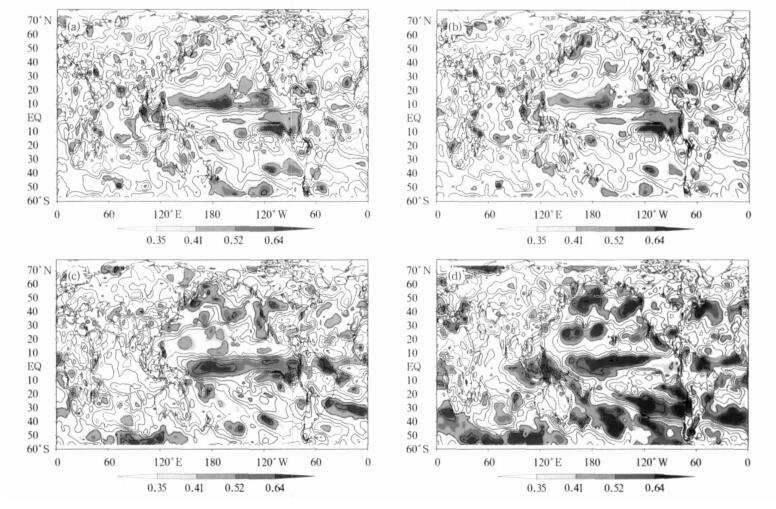
图 6 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的太平洋年代际振荡指数与夏季降水预报误差相关分析
Fig. 6 Same as in Fig.5, but for the Pacific decadal oscillation index
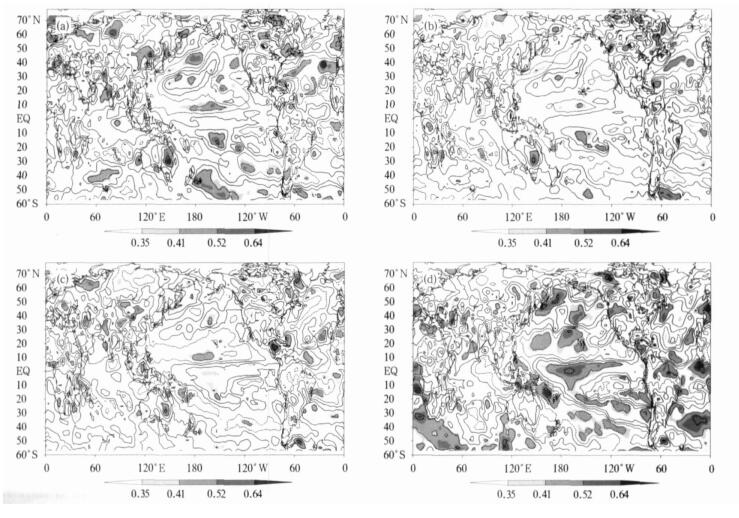
图 7 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的南半球环状模指数与夏季降水预报误差相关分析
Fig. 7 Same as in Fig.5, but for the Southern Hemispheric annular mode index
图 8 前期秋季 (a)、冬季 (b)、春季 (c) 和同期夏季 (d) 的北半球环状模指数与夏季降水预报误差相关分析
Fig. 8 Same as in Fig.5, but for the Northern Hemispheric annular mode index
-
[1] 王绍武.现代气候学研究进展.北京:气象出版社, 2001: 306-311. [2] 陈兴芳, 赵振国.中国汛期降水预测研究及应用.北京:气象出版社, 2000: 1-241. [3] 丑纪范, 徐明.短期气候数值预测的进展和前景.科学通报, 2001, 46(11): 890-895. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200111001.htm [4] 丁一汇, 刘一鸣, 宋永加, 等.我国短期气候动力预测模式系统的研究及试验.气候与环境研究, 2002, 7(2): 236-246. http://www.cnki.com.cn/Article/CJFDTOTAL-QHYH200202010.htm [5] 李维京, 张培群, 李清泉, 等.动力气候模式预测系统业务化及其应用.应用气象学报, 2005, 16(增刊): 1-11. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFD2005&filename=YYQX2005S1000&v=MTAzNTJUM3FUcldNMUZyQ1VSTDJmWk9SdEZ5dmdWTHpBUERUYWRyRzRIdFN2cm85RlpJUjhlWDFMdXhZUzdEaDE= [6] 丑纪范.为什么要动力-统计相结合?———兼论如何结合.高原气象, 1986, 5(4): 367-372. http://www.cnki.com.cn/Article/CJFDTOTAL-GYQX198604008.htm [7] 顾震潮.天气数值预报中过去资料的使用问题.气象学报, 1958, 29(3): 176-184. http://www.cnki.com.cn/Article/CJFDTOTAL-QXXB195803002.htm [8] 丑纪范.天气数值预报中使用过去资料的问题.中国科学, 1974, 17(6): 635-644. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK197406010.htm [9] 郑庆林, 杜行远.使用多时刻观测资料的数值天气预报新模式.中国科学, 1973, 16(2): 289-297. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK197303004.htm [10] 曹鸿兴.大气运动的自忆性方程.中国科学 (B辑), 1993, 23 (1): 104-112. http://www.cnki.com.cn/Article/CJFDTOTAL-JBXK199301014.htm [11] 邱崇践, 丑纪范.天气预报的相似-动力方法.大气科学, 1989, 13(1): 22-28. http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK198901002.htm [12] 黄建平, 王绍武.相似-动力模式的季节预报试验.中国科学 (B辑), 1991, 21(2): 216-224. http://www.cnki.com.cn/Article/CJFDTOTAL-JBXK199102013.htm [13] 张培群, 丑纪范.改进月延伸预报的一种方法.高原气象, 1997, 16(4): 376-388. http://www.cnki.com.cn/Article/CJFDTOTAL-GYQX704.005.htm [14] 谷湘潜.一个基于大气自忆原理的谱模式.科学通报, 1998, 43(1): 1-9. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTB199809002.htm [15] 曹鸿兴, 谷湘潜.自忆谱模式制作中期天气预报的试验.应用气象学报, 2000, 11(4) : 455-466. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20000467&flag=1 [16] 封国林, 曹鸿兴, 谷湘潜, 等.一种提高数值模式时间差分计算精度的新格式———回溯时间积分格式.应用气象学报, 2002, 13(2): 207-217. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20020227&flag=1 [17] 鲍名, 倪允琪, 丑纪范.相似-动力模式的月平均环流预报试验.科学通报, 2004, 49(11): 1112-1115. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200411017.htm [18] 任宏利, 丑纪范.统计-动力相结合的相似误差订正法.气象学报, 2005, 63(6): 988-993. http://www.cnki.com.cn/Article/CJFDTOTAL-QXXB200506014.htm [19] 任宏利, 丑纪范.在动力相似预报中引入多个参考态的更新.气象学报, 2006, 64(3): 315-324. http://www.cnki.com.cn/Article/CJFDTOTAL-QXXB200603005.htm [20] 丑纪范, 任宏利.数值天气预报———另类途径的必要性和可行性.应用气象学报, 2006, 10(2): 240-244. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20060240&flag=1 [21] 任宏利, 张培群, 李维京, 等.基于多个参考态更新的动力相似预报方法及应用.物理学报, 2006, 55(8): 4388-4396. http://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200608100.htm [22] 任宏利, 丑纪范.动力相似预报的策略和方法研究.中国科学 (D辑), 2007, 37(8): 1101-1109. http://www.cnki.com.cn/Article/CJFDTOTAL-JDXK200708014.htm [23] Barnett T P, Preisendorfer R. Origins and levels of monthly and seasonal forecast skill for United States surface air temperatures determined by canonical correlation analysis. Mon Wea Rev, 1987, 115: 1825-1850. doi: 10.1175/1520-0493(1987)115<1825:OALOMA>2.0.CO;2 [24] Zeng Q C, Zhang B L, Yuan C G, et al. A note on some methods suitable for verifying and correcting the prediction of climate anomaly.Adv Atmos Sci, 1994, 11(2): 121-127. doi: 10.1007/BF02666540 [25] Feddersen H, Navarra A, Ward A N. Reduction of model systematic error by statistical correction for dynamical seasonal predictions. J Climate, 1999, 12: 1974-1989. doi: 10.1175/1520-0442(1999)012<1974:ROMSEB>2.0.CO;2 [26] Wang H J, Zhou G Q, Zhao Y. An effective method for correcting the seasonal-interannual prediction of summer climate anomaly. Adv Atmos Sci, 2000, 17: 234-240. doi: 10.1007/s00376-000-0006-9 [27] Kang I S, Lee J Y, Park C K.Potential predictability of summer mean precipitation in a dynamical seasonal prediction system with systematic error correction. J Climate, 2004, 17:834-844. doi: 10.1175/1520-0442(2004)017<0834:PPOSMP>2.0.CO;2 [28] 郎咸梅, 王会军, 姜大膀.应用九层全球大气格点模式进行跨季度短期气候预测系统性试验.地球物理学报, 2004, 47(1): 19-24. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200401003.htm [29] Chen H, Lin Z H.A correction method suitable for dynamical seasonal prediction.Adv Atmos Sci, 2006, 23(3):425-430. doi: 10.1007/s00376-006-0425-3 [30] Mantua N J, Hare S R, Zhang Y, et al. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Amer Meteor Soc, 1997, 78: 1069-1079. doi: 10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2 [31] Li J, Wang J X L. A modified zonal index and its physical sense. Geophys Res Lett, 2003, 30(12), 1632, Doi: 10.1029/ 2003 GL017441 [32] Nan S, Li J. The relationship between summer precipitation in the Yangtze River valley and the previous Southern Hemisphere annular mode. Geophys Res Lett, 2003, 30(24), 2266 Doi: doi:10.1029/2003G L018381 [33] Li J, Wang J X L. A new North Atlantic Oscillation index and its variability. Adv Atmos Sci, 2003, 20(5): 661-676. doi: 10.1007/BF02915394 [34] 任宏利.短期气候预测中基于预报因子的误差订正方法研究.自然科学进展, 2007, 17(12): 1651-1656. http://www.cnki.com.cn/Article/CJFDTOTAL-ZKJZ200712007.htm -

 设为首页
设为首页 加入收藏
加入收藏


 下载:
下载: