基于Γ分布的气压序列非均一性检验方法初探
The Inhomogeneity Test Method of Atmospheric Pressure Sequences Based on Γ-distribution
-
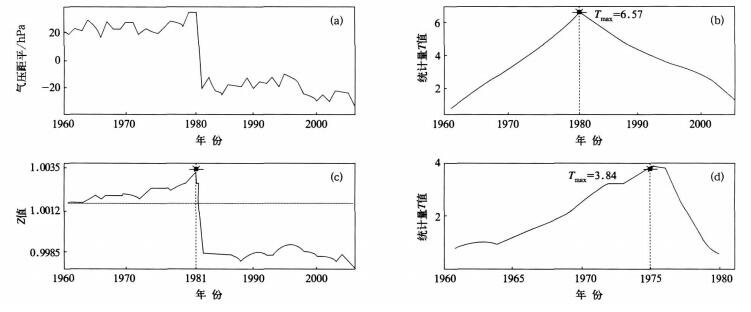
摘要: 通过对安徽省内23个代表台站1961—2006年平均气压序列均一性检验的研究,提出了一种基于Γ分布气压序列非均一性检验方法——Γ检验法。以桐城市数据为例,给出了检验和分析的具体过程,最后将该方法检验结果与常见的基于正态分布的SNHT法检验结果进行了对比分析,结果表明:该方法具有更广泛的使用范围和较高的准确性,可以检验大部分年平均气压的非均一性。检验结果表明:气压计高度的调整、台站迁址是安徽省内气压序列非均一性的主要原因。Abstract: Climate change research is built on the basis of homogeneity sequence data which can reflect the real changes. Therefore the homogeneity and/or the inhomogeneity of the meteorological observation data should be tested before using the data for climate change research. Currently, the main methods of homogeneity test are based on the hypothesis that the data sequences obey the normal distribution. However, in Anhui Province, it is found the average pressure sequence homogeneity test for 23 representative stations from 1961 to 2006 that some sequences are not subject to normal distribution, which can not be tested by the common method based on normal distribution. At the same time, it is found that some sequences obey Γ-distribution (pass the significant level of 0.05 Kolmogorov goodness of fit tests). A new homogeneity test method, Γ-test, for atmospheric pressure sequences is presented, in which the hypothesis should be met at first that the sequence is subject to Γ-distribution. Firstly, some reference stations are used to construct a reference sequence; then the ration sequences of stations which will be the test sequences to reference sequences are gotten; thirdly, the ration sequences are tested by Γ-test sequence homogeneity test; finally, the cause of the inhomogeneity sequences are analyzed by checking the history of the stations.The method is briefly introduced, and the data of Tongcheng are taken as an example, the concrete process of Γ-testing and analysis are given. Furthermore, the result of Γ-test is compared with SNHT which is a widely use method. The results show that the 23 stations can be tested by Γ-test and the accuracy rate reaches 78.3%. In contrast, four stations can not be tested by SNHT and the accuracy only reaches 53.8%. In other words, Γ-test is superior to SNHT in scope and accuracy. Nevertheless, Γ-test also has some problems such as the high computational complexity and missing of some change points. The Homogeneity test results show that the change of barometer height and the station location is the main reason of the significant inhomogeneity of atmospheric pressure sequences in An hui Province.
-
表 1 不同n值时T95的值
Table 1 The value of T95 in different n

表 2 Γ检验与SNHT检验结果及原因分析
Table 2 The results and causes of Γ-test and SNHT

表 3 变点个数统计
Table 3 The number of change points

-
[1] 屠其璞, 王俊德, 丁裕国, 等.气象应用概率统计学, 北京:气象出版社, 1984: 488-489. [2] Alexandersson H.A homogeneity test applied to precipitation data.International Journal of Climatology, 1986, 6:661-675. doi: 10.1002/joc.v6:6 [3] Easterling D R, Peterson T C.A new method for detecting and adjusting for undocumented in climatological time series.International Journal of Climatology, 1995, 15:369-377. doi: 10.1002/joc.3370150403/abstract [4] Potter K W.Illustration of a new test for detecting a shift in mean in precipitation series.Mon Wea Rev, 1981, 109: 2040-2045. https://www.researchgate.net/publication/241241450_Illustration_of_a_New_Test_for_Detecting_a_Shift_in_Mean_in_Precipitation_Series [5] 刘小宁, 孙安健.年降雨量序列非均-性检验方法探讨.气象, 1995, 21(8): 3-6. [6] 宋超辉, 刘小宁, 李集明.气温序列非一均性检验方法研究.应用气象学报, 1995, 6(3): 289-296. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=19950346&flag=1 [7] 鞠晓慧, 屠其璞, 李庆祥.我国太阳总辐射月总量资料的均一性检验及订正.南京气象学院学报, 2006, 29(3): 336-341. http://www.cnki.com.cn/Article/CJFDTOTAL-NJQX200603006.htm [8] Buishand T A.Some methods for testing the homogeneity of rainfall records.Journal of Hydrology, 1982, 58: 11-27. doi: 10.1016/0022-1694(82)90066-X [9] Worsley K J.On the likelihood ratio test for a shift in location of normal populations.Journal of the American Statistical Association, 1979, 74: 365-367. https://www.researchgate.net/publication/265352400_On_the_Likelihood_Ratio_Test_for_a_Shift_in_Location_of_Normal_Populations [10] Hsu D A.Detecting shifts of parameter in Gamma sequences with applications to stock price and air traffic flow analysis.Journal of the American Statistical Association, 1979, 74: 31-40. https://www.researchgate.net/publication/254285245_Detecting_Shifts_of_Parameter_in_Gamma_Sequences_with_Applications_to_Stock_Price_and_Air_Traffic_Flow_Analysis [11] 谭常春, 赵林城, 缪柏其.至多一个变点的Γ分布的统计推断及在金融中的应用.系统科学与数学, 2007, 27(1): 2-10. http://www.cnki.com.cn/Article/CJFDTOTAL-STYS200701002.htm [12] 谭常春, 缪柏其.至多一个变点Γ分布的统计推断.中国科技大学学报, 2005, 35(1): 51-58. http://www.cnki.com.cn/Article/CJFDTOTAL-ZKJD200501006.htm [13] 谭常春.变点问题统计推断及其在金融中的应用.合肥:中国科技大学, 2007. [14] 孙俊锁. Gamma分布的特征函数及点估计.鞍山钢铁学院院报, 2001, 24(2): 125-129. http://www.cnki.com.cn/Article/CJFDTOTAL-ASGT200102013.htm [15] 黄嘉佑.气象统计分析与预报方法(第三版).北京:气象出版社, 2004: 23-25. [16] 苏金明, 阮沈用. Matlab 6.1实用指南 (下册).北京:电子工业出版社, 2002: 413-416. -

 设为首页
设为首页 加入收藏
加入收藏


 下载:
下载:
