设为首页
加入收藏
The Optimized Design of Stack for GRAPES's Adjoint Mode
-
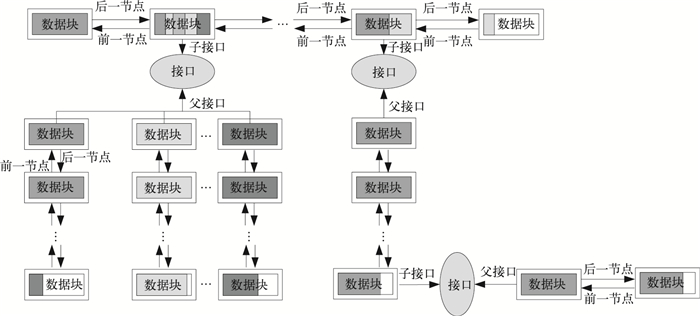
摘要: GRAPES伴随模式是其四维变分同化系统的核心组成部分。由于其计算过程复杂，临时数据较多，实现中采用断点存储策略可以有效减少伴随模式的计算时间和存储空间。极限断点存储策略是在单积分步内以全存储策略实现为基础，将其中部分基态以计算代替的一种类断点存储策略。在该策略的支持下，需要一种新的数据管理结构，来保证程序的正确运行。文章提出了在已有栈基础上优化的新数据存储管理方式——嵌套多链栈，这种结构可有效满足使用极限断点存储技术实现GRAPES伴随模式的初态管理需求。试验表明：相比断点存储技术，在总内存增加不超过30%的情况下可使GRAPES的运行效率提高1倍。Abstract: The four dimensional variational data assimilation system (4DVAR) of GRAPES (Global/Region Assimilation and Prediction System) can use different meteorological data from different areas of different times obtained to optimize the quality of forecast based on an initialization background. As the core of the 4DVAR, tangent mode and adjoint mode can adjust the initialization background through using the deviation of the estimate of 3DVAR and observation.When a segment of the adjoint mode is run, the initial state of corresponding nonlinear mode might be needed as input. In order to balance the disadvantage of whole storage and whole computation, a double chained stack is used to store an interim data's snap for implementing the adjoint mode. Adopting the whole storage can speed up the adjoint mode prominently, but this may lead to the relation of first in and first out (FIFO) among some data blocks, which conflicts with the configuration of the double chained stack. A nested and double chained stack is proposed based on original double chained stack, using a kid chained stack to separate the data blocks that have FIFO relations. Data block pops first must be pushes in kid chained stack, and then can be popped at any time as needed. The nested and double chained stack can meet these requirements of different data blocks, FIFO or FILO, and satisfy the requirement of adjoint mode better. The result of experiment shows these approaches can double the operational speed with 30% extra memory.
-
Key words:
- GRAPES;
- adjoint mode;
- optimization;
- nested and double chained stack
-
图 3 GRAPES模式6 h预报的850 hPa位势高度 (单位: gpm) (a) 优化前结果，(b) 优化后结果
Fig. 3 An example of 6-hour 850 hPa geo-potential height forecast of GRAPES (unit: gpm)
(a) the result before optimization, (b) the result after optimization
图 4 GRAPES伴随模式运行内存占用动态图
(a) 优化前后临时数据保存总量动态图，(b) 优化前后伴随模式占用内存总量动态图
Fig. 4 The dynamic memory consumption of GRAPES adjiont mode
(a) total amount of temporary data storage before and after optimization, (b) total memory consumption of adjoint mode before and after optimization
表 1 优化前后对比
Table 1 The result before and after optimization
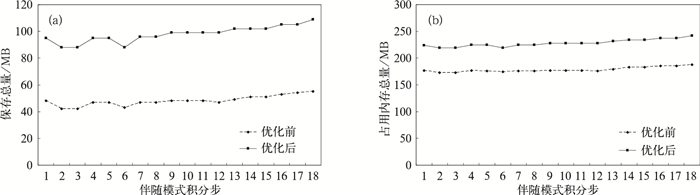
时间 堆栈最大值/MB 程序占用总内存/MB ad_integrat执行时间/s 优化前 约55 约200 49.79 优化后 约110 约255 24.10 
下载: 导出CSV
-
[1] 薛纪善.新世纪初我国数值天气预报的科技创新研究.应用气象学报, 2006, 17(5):601-610. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200605103&flag=1 [2] Chen Dehui, Xue Jishan. GRAPES-CMA's New Generation of Weather and Climate Model: Scientific Design and Development Progresses. Proceedings of the 2004 Workshop on the Solution of Partial Differential Equations on the Sphere, 2004. [3] Xue Jishan. Progresses of researches on numerical weather prediction in China: 1999—2002. Adv Atmos Sci, 2005, 21(3):467-474. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dqjz200403015&dbname=CJFD&dbcode=CJFQ [4] 张华, 薛纪善, 庄世宇. GRAPES三维变分同化系统得理想试验.气象学报, 2004, 62(1):31-41. doi: 10.11676/qxxb2004.004 [5] 庄世宇, 薛纪善, 朱国富, 等. GRAPES全球三维变分同化系统——基本设计方案与理想试验.大气科学, 2005, 29(6):872-884. http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK200506003.htm [6] Xue Jishan. Development of 3DVAR for Operational Application in CMA. Proceedings of 4th WMO International Symposium on Assimilation of Observations in Meteorology and Oceanography, WMO/TD-No.1316, Geneva: WMO, 2005. [7] 陈德辉, 杨学胜, 胡江林, 等.多尺度通用动力模式框架的设计策略.应用气象学报, 2003, 14(4): 452-461. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20030456&flag=1 [8] 薛纪善, 陈德辉.数值预报系统GRAPES的科学设计与应用.北京:科学出版社, 2008:54-60. [9] 张林, 朱宗申. GRAPES模式切线性垂直扩散方案的误差分析和改进.应用气象学报, 2008, 19(2):194-200. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20080235&flag=1 [10] 陈德辉, 沈学顺.新一代数值预报系统GRAPES的研究进展.应用气象学报, 2006, 17(6):773-777. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200606125&flag=1 [11] 伍湘君, 金之雁, 陈德辉, 等.新一代数值预报模式GRAPES的并行计算方案设计与实现.计算机研究与发展, 2007, 44(3):510-515. http://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ200703020.htm [12] 伍湘君, 金之雁, 黄丽萍, 等. GRAPES模式软件框架与实现.应用气象学报, 2005, 16(4):539-546. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20050468&flag=1 [13] 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现.应用气象学报, 2005, 16(3):374-384. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20050346&flag=1 [14] Laurent Hascoet, Valerie Pascual. TAPENADE 2.1 User's Guide. 2004. hhtp://tapenade.inria.fr:8080/tapenade/index.jsp. [15] 陈峰峰, 王光辉, 沈学顺, 等. Cascade插值方法在GRAPES模式中的应用.应用气象学报, 2009, 20(2):164-170. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20090205&flag=1 -
图(4) / 表(1)
计量
- 摘要浏览量: 4312
- HTML全文浏览量: 906
- PDF下载量: 1138
- 被引次数: 0
