设为首页
加入收藏
Statistical Estimation of Dynamic Balance Constraints in GRAPES Variational Data Assimilation System
-
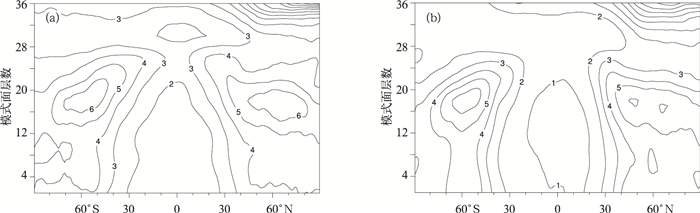
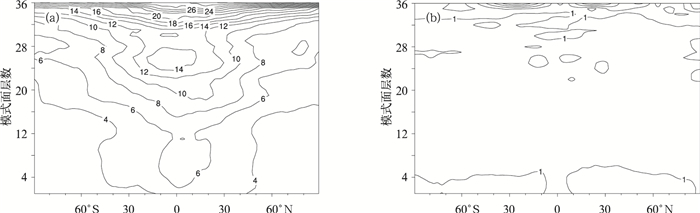
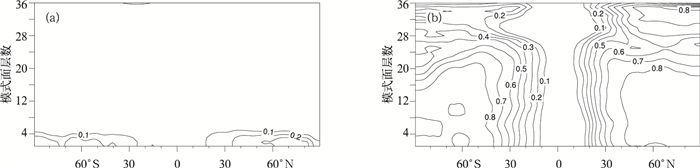
摘要: 该文在GRAPES (Global/Regional Assimilation and PrEdiction System) 模式面三维变分 (3D_Var) 框架中引入了一种描述不同控制变量之间动力平衡约束的新方案。新方案采用统计得到的流函数和模式气压变量 ( π ) 之间的回归系数代替原方案中的线性平衡方程，来表达旋转风和质量场之间的平衡关系；采用流函数和势函数之间的回归系数，补充表达了原方案中所没有的旋转风和散度风之间的平衡关系。与原方案相比，新方案算法简单，避免了垂直方向的反复插值，减少了插值误差的引入。通过随机扰动试验和单点试验可以发现，在地转关系成立较好的区域，新方案中旋转风和质量场的耦合程度与原方案接近一致；而在地转关系不适用区域，新方案可以有效减小两者的耦合程度。此外，由于新方案中添加了旋转风和散度风之间的动力平衡约束，边界层的风场分析也更加接近大气真实状况。Abstract: Dynamic balance constraints that govern the atmospheric circulation play very important roles in the analysis of atmospheric state. These constraints indicate how it might be possible to determine one variable from another. As a result, they could help to avoid noise caused by gravity waves, and enable maximum information to be extracted from the observations.The existing GRAPES three-dimensional variational data assimilation system, which is defined on sigma coordinates, uses linear balance equation to ensure that mass and wind analysis increments to be geostrophically coupled. In this formulation, to deal with difficulties in solving the balance equation at sigma levels, analysis variables need to be interpolated to a series of auxiliary isobaric surface to calculate balanced components. A new formulation of estimating dynamic balance constraints is developed in the variation assimilation system. In the new scheme, regression coefficients between stream function and dimensionless pressure (Exner function), instead of the geostrophic balance equation in the original scheme, is used to describe the balance relationship between rotational wind and mass field. In addition, the balance relationship between rotational wind and divergent wind is similarly described by regression coefficients between stream function and velocity potential. Compared to the old scheme, the new formulation avoids repeated interpolations along the vertical direction, which would make the estimation simpler and more accurate.In the new formulation, the balanced coefficients are computed using NMC method, which is found to produce a useful approximation to the true balance constraints in atmosphere. Based on 24 h, 48 h GRAPES forecast differences, linear regression is carried out for each level and for each latitude. By doing this an implied latitude-dependent structure in the dimensionless pressure is directly included in the analysis. Statistical results show that the explained variance of dimensionless pressure is primarily in the extratropics with the variance best explained below 100 hPa in this new formulation. And the explained velocity potential ratio has a maximum in the middle and high latitudes near the surface. Results of randomization and single-observation experiments indicate that, in regions where geostrophic balance is appropriate, the new formulation behaves similarly to the original scheme. However, in regions where geostrophic balance is not appropriate, the new formulation could allow for a smooth decoupling of stream function and dimensionless pressure, while the original scheme can not. Such properties of the new formulation could help variational data assimilation system get more reasonable analysis results in tropics and tropopause. Moreover, by adding the balance relationship between rotational wind and divergent wind, the new formulation could derive a more reasonable wind field in boundary layer.
-
Key words:
- GRAPES;
- 3D_Var system;
- dynamical balance constraint;
- linear regression
-
图 1 变量平衡部分对总体方差解释率的纬向平均分布(a) 势函数，(b) 无量纲气压
Fig. 1 Zonal average of the explained variance ratios of velocity potential (a) and dimensionless pressure (b)
图 2 随机扰动方法模拟的无量纲气压的背景误差均方差的纬向平均分布 (单位：10-4)
(a) 原方案，(b) 新方案
Fig. 2 Zonal average of simulated background error standard deviations of dimensionless pressure in the original scheme (a) and the new scheme (b)(unit: 10-4)
图 3 随机扰动方法模拟的新方案中势函数背景误差均方差的纬向平均分布 (单位：106m2·s-1)
(a) 势函数全量，(b) 势函数的平衡部分
Fig. 3 Zonal average of simulated background error standard deviations of velocity potential (a) and its balance part (b) in the new scheme (unit: 106m2·s-1)
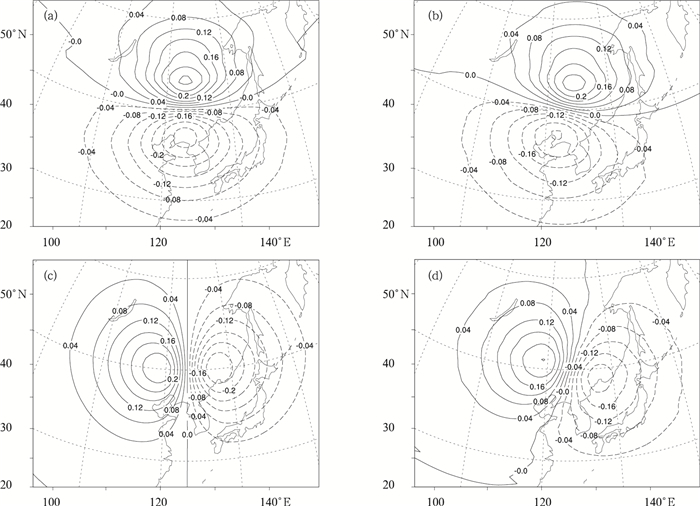
图 4 理想u观测 (高出背景场5 m·s-1) 位于模式面第12层45.5°N, 125.5°E时强迫出的无量纲气压分析增量 (单位：10-5)
(a) 原方案水平分布，(b) 新方案水平分布，(c) 原方案经向垂直分布，(d) 新方案经向垂直分布
Fig. 4 Dimensionless pressure increments generated by a simulated u component wind observation on the 12th model level at 45.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit: 10-5)
(a) horizontal distribution of the original scheme, (b) horizontal distribution of the new scheme, (c) meridional section of the original scheme, (d) meridional section of the new scheme
图 5 理想u观测 (高出背景场5 m·s-1) 位于模式面第24层的45.5°N，125.5°E时强迫出的无量纲气象分析增量水平分布 (单位：10-5)(a) 原方案，(b) 新方案
Fig. 5 Dimensionless pressure increments generated by a simulated u component wind observation on the 24th model level at 45.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit: 10-5)
(a) horizontal distribution of the original scheme, (b) horizontal distribution of the new scheme
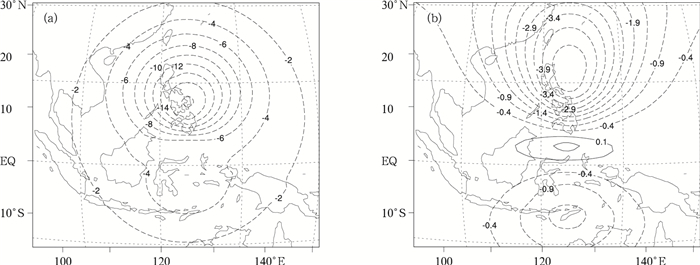
图 6 理想u观测 (高出背景场5 m·s-1) 位于模式面第12层的5.5°N，125.5°E时强迫出的无量纲气压分析增量的水平分布 (单位：10-6)(a) 原方案，(b) 新方案
Fig. 6 Dimensionless pressure increments generated by a simulated u component wind observation on the 12th model level at 5.5°N, 125.5°E which is 5 m·s-1stronger than background wind (unit:10-6)
(a) horizontal distribution of the original scheme, (b) horizonal distribution of the new scheme
图 7 理想气压观测 (高出背景场1 hPa) 位于模式面第1层45.5°N，125.0°E时强迫出的水平风场u, v的分析增量水平分布 (单位：m·s-1)
(a)原方案u增量，(b) 新方案u增量，(c) 原方案v增量，(d) 新方案v增量
Fig. 7 Wind increments generated by a simulated pressure observation on the first model level at 45.5°N, 125.0°E which is 1 hPa higher than the background (unit:m·s-1)
(a)u increment of the original scheme, (b)u increment of the new scheme, (c)v increment of the original scheme, (d)v increment of the new scheme
表 1 12月、1月和2月GRAPES模式面对应气压
Table 1 Roughly corresponding pressure values of GRAPES model levels in Dec, Jan and Feb
模式面 全球平均气压/hPa 第4层 900 第8层 740 第12层 566 第16层 403 第20层 262 第24层 153 第28层 69 第32层 26 第36层 8.8 
下载: 导出CSV
-
[1] Daley R. Atmospheric Data Analysis. Cambridge: Cambridge University Press, 1991: 2-6; 107-118. [2] Kalnay E. Atmospheric modeling, data assimilation and predictability. Cambridge: Cambridge University Press, 2003: 186-190. [3] Lönnberg P, Hollingsworth A. The statistical structure of short-range forecast errors as determined from radiosonde data Part Ⅱ: The covariance of height and wind errors. Tellus, 1986, 38A: 137-161. doi: 10.1111/tela.1986.38A.issue-2 [4] Courtier P, Talagrand O. Variational assimilation of meteorological observations with direct and adjoint shallow-water equations. Tellus, 1990, 42A: 531-549. doi: 10.3402/tellusa.v42i5.11896 [5] 薛纪善.新世纪初我国数值天气预报的科技创新研究.应用气象学报, 2006, 17(5): 602-610. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200605103&flag=1 [6] 曾智华, 马雷鸣, 梁旭东, 等. MM5数值预报引入GRAPES三维变分同化技术在上海地区的预报和检验.应用气象学报, 2004, 15(5): 534-542. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20040566&flag=1 [7] Parrish D F, Derber J C. The national meteorological center's spectral statistical interpolation analysis system. Mon Wea Rev, 1992, 120: 1747-1763. doi: 10.1175/1520-0493(1992)120<1747:TNMCSS>2.0.CO;2 [8] Lorenc A. A global three-dimensional multivariate statistical interpolation scheme. Mon Wea Rev, 1981, 109: 701-721. doi: 10.1175/1520-0493(1981)109<0701:AGTDMS>2.0.CO;2 [9] Derber J, Bouttier F. A reformulation of the background error covariance in the ECMWF global data assimilation system. Tellus, 1999, 51A: 195-221. doi: 10.1034/j.1600-0870.1999.t01-2-00003.x/citedby [10] Wu W S, Purser R J, Parrish D F. Three-dimensional variational analysis with spatially inhomogeneous covariances. Mon Wea Rev, 2002, 130: 2905-2916. doi: 10.1175/1520-0493(2002)130<2905:TDVAWS>2.0.CO;2 [11] Barker M D, Huang W, Guo Y R, et al. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon Wea Rev, 2004, 132: 897-914. doi: 10.1175/1520-0493(2004)132<0897:ATVDAS>2.0.CO;2 [12] Lorenc A, Ballard S P, Bell R S, et al. The Met. Office global three-dimensional variational data assimilation scheme. Q J R Meteorol Soc, 2000, 126: 2991-3012. doi: 10.1002/(ISSN)1477-870X [13] 朱乾根, 林景瑞, 寿绍文, 等.天气学原理和方法.北京:气象出版社, 2000: 22-59. [14] 庄世宇, 薛纪善, 朱国富, 等. GRAPES全球三维变分同化系统——基本设计方案与理想试验.大气科学, 2005, 29(6): 872-884. http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK200506003.htm [15] 马旭林, 庒照荣, 薛纪善, 等. GRAPES非静力数值预报模式的三维变分同化系统的发展.气象学报, 2009, 67(1): 50-60. doi: 10.11676/qxxb2009.006 [16] 陈德辉, 杨学胜, 张红亮, 等.多尺度非静力通用模式框架的设计策略.应用气象学报, 2003, 14(4): 452-461. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20030456&flag=1 [17] 黄丽萍, 伍湘君, 金之雁. GRAPES模式标准初始化方案设计与实现.应用气象学报, 2005, 16(3): 374-384. doi: 10.11898/1001-7313.20050312 [18] 陈德辉, 沈学顺.新一代数值预报系统GRAPES研究进展.应用气象学报, 2006, 17(6): 773-777. doi: 10.11898/1001-7313.20060614 [19] Bannister R N. A review of forecast error covariance statistics in atmospheric variational data assimilation. Ⅱ: Modelling the forecast error covariance statistics. Q J R Meteorol Soc, 2008, 134: 1971-1996. doi: 10.1002/qj.v134:637 [20] 薛纪善, 陈德辉.数值预报系统GRAPES的科学设计与应用.北京:气象出版社, 2008: 6-11. [21] Bannister R N. A review of forecast error covariance statistics in atmospheric variational data assimilation. Ⅰ: Characteristics and measurements of forecast error covariances. Q J R Meteorol Soc, 2008, 134: 1951-1970. doi: 10.1002/qj.v134:637 [22] 成秋影.天气分析和诊断方法.北京:气象出版社, 1992: 152-156. [23] 沈桐立, 田永祥, 葛孝贞, 等.数值天气预报.北京:气象出版社, 2003: 267-293. [24] Ingleby N B. The statistical structure of forecast errors and its representation in the met office global 3-D variational data assimilation scheme. Q J R Meteorol Soc, 2001, 127: 209-231. doi: 10.1002/(ISSN)1477-870X [25] Andersson E, Fisher M, Munro R, et al. Diagnosis of background errors for radiances and othe observable quantities in a variational data assimilation scheme, and the explanation of case of poor convergence. Q J R Meteorol Soc, 2000, 126: 1455-1472. doi: 10.1256/smsqj.56511 -
计量
- 摘要浏览量: 4226
- HTML全文浏览量: 1107
- PDF下载量: 1630
- 被引次数: 0
