设为首页
加入收藏
Application of Spline Interpolation to Physical Process Feedback Accuracy Improvement of GRAPES Model
-
摘要: GRAPES (Global/Regional Assimilation and PrEdiction System) 模式动力框架中垂直方向变量的跳层设置采用Charney-Phillips分布，在整层上进行位温、水物质的计算，物理过程中在半层上对其进行处理。这样在GRAPES模式中，进入物理过程之前和物理过程计算完毕之后，都要采用线性插值进行整层和半层之间物理量的转换。由于线性插值精度欠佳，为提高上述反馈过程的精度，并保证水物质的正定性，该研究引入样条插值，并在水物质的插值过程中进行保单调处理，有效减小了位温场、水物质场的预报偏差，并提升了模式的综合预报性能。Abstract: The variable distribution in the vertical direction of GRAPES model's dynamic core adopts Charney-Phillips method. Vertical velocity, potential temperature, water substance are calculated at the whole layer, horizontal velocity and dimensionless pressure are calculated at the half layer, but in physical process, all the variables are placed on the half layer. In order to satisfy the needs of the central difference calculations and better representation of the physical processes in the boundary layer, a nonuniform stratification is adopted, which is dense near the ground, and the higher the more sparse. Therefore, in GRAPES model, linear interpolation is needed to convert variables between whole and half layers before and after the physical process calculation.For the weather prediction model of various international centers, Lorenz layers are used in the physical part and all the variables are on the half layer. Most models also use Lorenz layers in the dynamic core, except for the Unified Model of the UK Meteorological Office, which chooses Charney-Philips layer for dynamic core and uses linear interpolation in dealing with the similar problem of interpolation between whole and half layers.Linear interpolation is relatively simple, but the accuracy is not high, and it will cause deviation especially for lower and higher layers. The cumulative deviation in the temperature and humidity fields will further impact the height and wind fields. In addition, the interpolation process of water substance is also required to ensure monotonic, but the traditional cubic spline interpolation, polynomial interpolation, cannot be guaranteed monotonic, which will bring negative water, instability and other issues.In order to solve the problems above, the traditional cubic spline interpolation method is introduced for potential temperature interpolation in GRAPES model. After some special handling of the boundary value based on the traditional one, a monotonic cubic spline interpolation method is established for water substance, by which the forecast error of potential temperature and humidity fields in the GRAPES model is effectively reduced. The feedback accuracy of physical process is improved, and the model comprehensive performance is also enhanced.
-
Key words:
- GRAPES model;
- linear interpolation;
- spline interpolation;
- monotonic
-
图 2 3种不同算法对给定分布的模拟
Fig. 2 Three different algorithms on the given distribution simulation
图 3 插值前后长江中下游平原示例点 (30°N, 115°E) 偏差的垂直分布 (a) 位温场，(b) 水汽场
Fig. 3 The deviation vertical distribution after interpolation at the sample point (30°N, 115°E) over the Yangtze River Plain (a) the potential temperature, (b) the water vapor
图 4 插值前后北半球中纬度地区 (20°~60°N) 均方根误差的区域平均的垂直分布
(a) 位温场, (b) 水汽场
Fig. 4 The regional averaged root mean square error vertical distribution after interpolation of the Northern Hemisphere mid-latitude region (20°—60°N)
(a) the potential temperature, (b) the water vapor
图 5 插值前后位温场均方根误差的全球纬向平均垂直剖面 (单位：℃)
(a) 线性插值, (b) 传统的三次样条插值
Fig. 5 The zonal mean vertical distribution of temperature root mean square error after interpolation (unit:℃)
(a) linear interpolation, (b) traditional cubic spline interpolation
图 6 插值前后水汽场均方根误差的全球纬向平均垂直剖面 (单位：g·kg-1)
(a) 线性插值, (b) 单调的三次样条插值
Fig. 6 The zonal mean vertical distribution of water vapor root mean square error after interpolation (unit:g·kg-1)
(a) linear interpolation, (b) monotonic cubilc spline interpolation
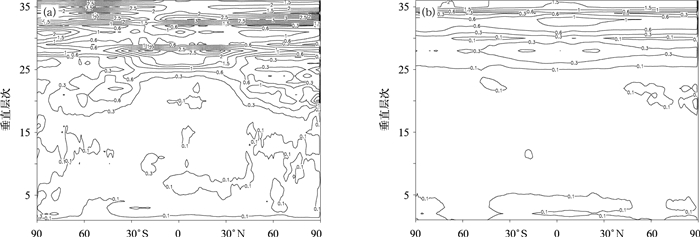
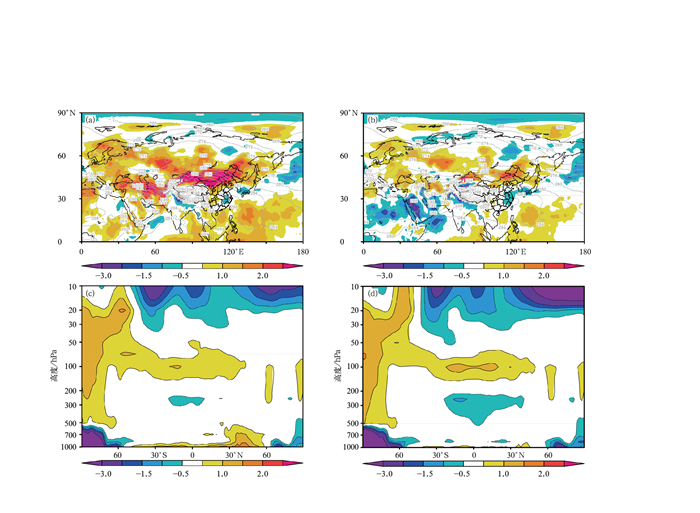
图 7 2009年7月7—20日批量试验72 h温度场预报与FNL的平均偏差 (单位:K，阴影为偏差，灰线为预报场)
(a) 线性插值700 hPa的偏差，(b) 传统的三次样条插值700 hPa的偏差，(c) 线性插值偏差的纬向平均垂直剖面, (d) 传统的三次样条插值偏差的纬向平均垂直剖面
Fig. 7 Average deviation of 72-hour temperature forecast from bulk test against FNL data during 7—20 July 2009(unit:K, shaded for deviation, gray line for forecast field)
(a) linear interpolation of 700 hPa deviation field, (b) traditional cubic spline interpolation of 700 hPa deviation field, (c) zonal mean deviation vertical profile of linear interpolation, (d) zonal mean deviation vertical profile of traditional cubic spline interpolation
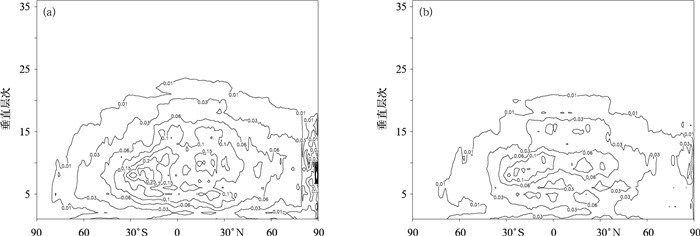
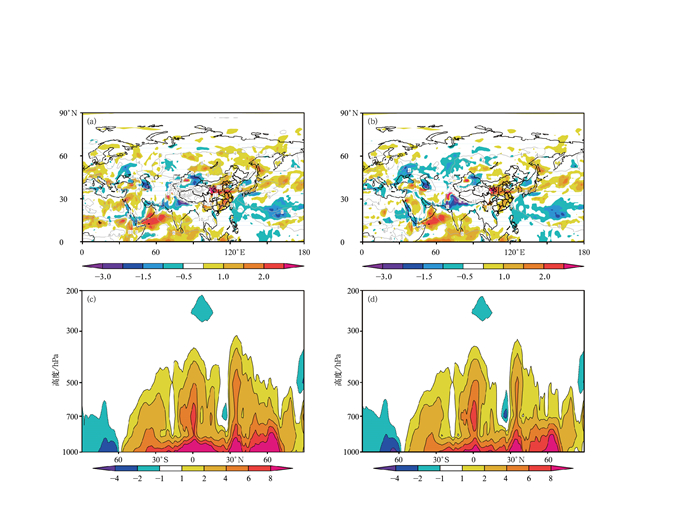
图 8 2009年7月7—20日批量试验72 h湿度场预报与FNL的偏差 (单位:g·kg-1, 图中阴影为偏差，灰线为预报场)
(a) 线性插值700 hPa的偏差，(b) 单调的三次样条插值700 hPa的偏差，(c) 线性插值偏差的纬向平均垂直剖面, (d) 单调的三次样条插值偏差的纬向平均垂直剖面
Fig. 8 Average deviation of 72-hour humidity forecast from bulk test against FNL data during 7—20 July 2009 (unit:g·kg-1, shaded for deviation, gray line for forecast field)
(a) linear interpolation of 700 hPa deviation field, (b) monotonic cubic spline interpolation of 700 hPa deviation field, (c) zonal mean deviation vertical profile of linear interpolation, (d) zonal mean deviation vertical profile of monotonic cubic spline interpolation
-
[1] 陈德辉, 沈学顺.新一代数值预报系统GRAPES研究进展.应用气象学报, 2006, 17(6): 773-777. doi: 10.11898/1001-7313.20060614 [2] 伍湘君, 金之雁, 黄丽萍, 等.GRAPES模式软件框架与实现.应用气象学报, 2005, 16(4): 539-546. doi: 10.11898/1001-7313.20050415 [3] 黄丽萍, 伍湘君, 金之雁.GRAPES模式标准初始化方案设计与实现.应用气象学报, 2005, 16(3): 374-384. doi: 10.11898/1001-7313.20050312 [4] 李兴良, 陈德辉, 沈学顺.不同垂直坐标系对垂直速度计算的影响.热带气象学报, 2005, 21(3): 265-276. http://www.cnki.com.cn/Article/CJFDTOTAL-RDQX200503005.htm [5] 陈德辉, 杨学胜, 张红亮, 等.多尺度非静力通用模式框架的设计策略.应用气象学报, 2003, 14(4): 452-461. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20030456&flag=1 [6] 胡江林, 沈学顺, 张红亮, 等.GRAPES模式动力框架的长期积分特征.应用气象学报, 2007, 18(3): 276-284. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20070349&flag=1 [7] 陈德辉, 薛纪善, 杨学胜, 等.GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究.科学通报, 2008, 20:2396-2407. doi: 10.3321/j.issn:0023-074X.2008.20.002 [8] 徐国强, 陈德辉, 薛纪善, 等.GRAPES物理过程的优化试验及程序结构设计.科学通报, 2008, 53(20): 2428-2434. doi: 10.3321/j.issn:0023-074X.2008.20.006 [9] 薛海乐, 沈学顺, 苏勇.地形湍流拖曳力参数化及在GRAPES中的应用.应用气象学报, 2011, 22(2): 169-181. doi: 10.11898/1001-7313.20110206 [10] Davies T, Cullen M J P, Malcolm A J, et al.A new dynamical core for the Met Office's global and regional modeling of the atmosphere.Q J R Meteorol Soc, 2005, 131:1759-1782. doi: 10.1256/qj.04.101 [11] Cote J S, Methot A, Patoine A, et al.The operational CMC-MRB Global Environmental Multiscale (GEM) model.Part Ⅰ:Desgin considerations and formulation.Mon Wea Rev, 1998, 126:1373-1395. doi: 10.1175/1520-0493(1998)126<1373:TOCMGE>2.0.CO;2 [12] Seity Y, Brousseau P, Malardel S, et al.The AROME-France Convective-Scale Operation Model.Mon Mea Rev, 2011, 139:976-991. https://www.researchgate.net/publication/258537490_The_AROME-France_convective-scale_operational_model [13] 宇如聪, 徐幼平.AREM暴雨数值预报模式.北京:中国科学院大气物理研究所, 2004. [14] Skamarock W C, Klemp J B, Dudhia J, et al.A Descriotion of the Advanced Research WRF Version 3.NCAR Technical Note, 2008. http://www.oalib.com/references/13162859 [15] IFS Documentation-Cy37r2 Operational Implementation 18 May 2011, Part Ⅲ:Dynamics and Numerical Procedures.ECMWF, 2011. [16] Staniforth A, White A, Wood N, et al.Unified Model Documentation Paper No.15, Joy of U.M.6.3-Model Formulation.UKMO, 2006. [17] 苏勇, 沈学顺.相变修正方案在GRAPES模式标量平流中的应用.气象学报, 2009, 67(7): 1089-1100. http://www.cnki.com.cn/Article/CJFDTOTAL-QXXB200906020.htm [18] 严家明, 刘诗斌, 李辉.线性插值的误差计算方法研究.弹箭与制导学报, 2005, 25(4): 111-112. http://www.cnki.com.cn/Article/CJFDTOTAL-DJZD200504037.htm [19] 阎洪.气候时空数据的样条插值与应用.地理与地理信息科学, 2003, 19(5): 27-31. http://www.cnki.com.cn/Article/CJFDTOTAL-DLGT200305007.htm [20] 狄扬波.应用样条插值方法对湿度场进行客观分析的尝试.热带气象, 1985, 1(1): 74-79. http://www.cnki.com.cn/Article/CJFDTOTAL-RDQX198501008.htm [21] Kruger C J C.Constrained Cubic Spline Interpolation.2003.http://www.korf.co.uk/spline.pdf. -
下载:
计量
- 摘要浏览量: 3322
- HTML全文浏览量: 1169
- PDF下载量: 1241
- 被引次数: 0
