Boundary Layer Coupling to Charney-Phillips Vertical Grid in GRAPES Model
-
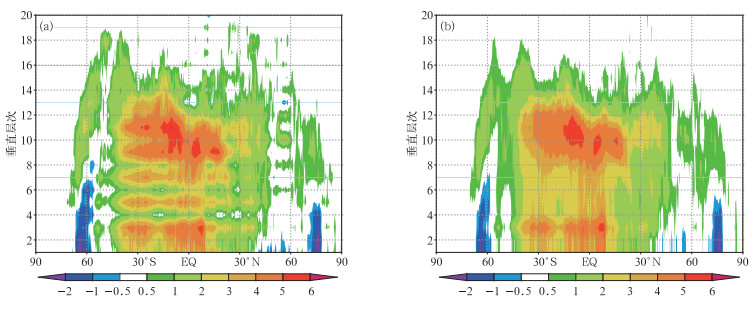
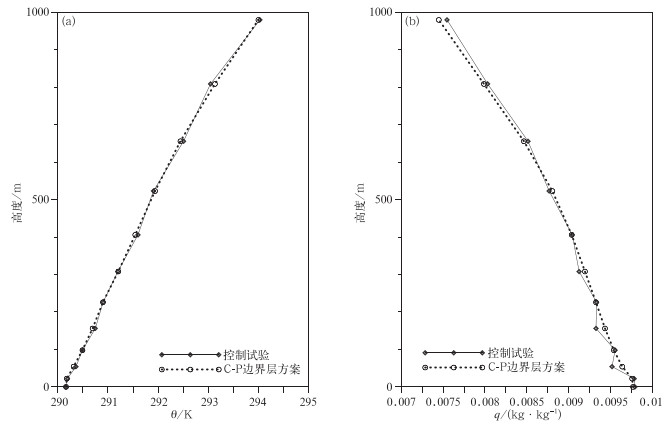
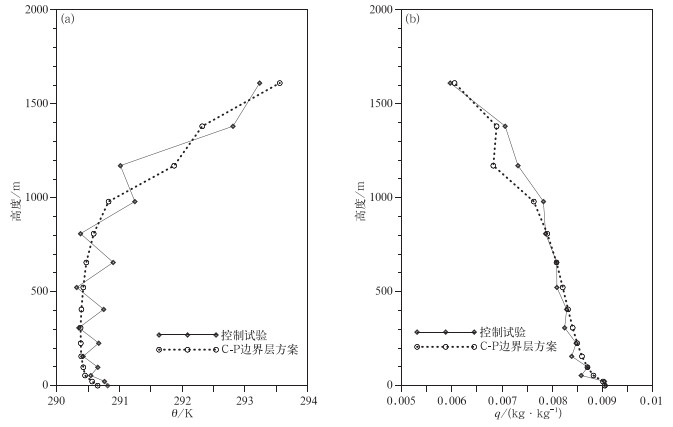
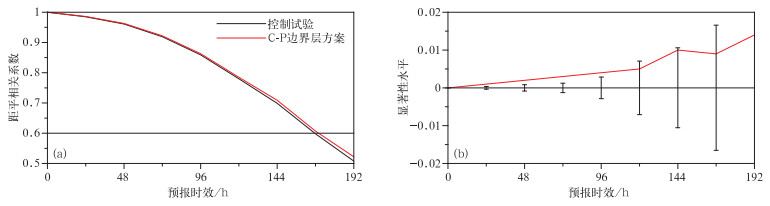
摘要: 基于K廓线闭合方案,通过考虑不稳定边界层和稳定边界层中热量交换系数在半层上求取及下边界条件的设置,将温湿倾向在整层上直接计算,设计了Charney-Phillips跳点(简称C-P跳点)的边界层方案,使之与GRAPES全球模式的C-P跳点相协调,解决了Lorenz跳点物理过程与C-P跳点动力框架耦合时插值造成的不协调问题,同时避免了耦合时反复插值造成的误差,提高了边界层物理过程参数化方案及其反馈的准确性和合理性。试验表明:C-P跳点边界层方案因为避免了温度和湿度在垂直方向上的插值,消除了温湿变量在垂直方向上的锯齿状抖动,使温湿廓线分布更合理,减小了模式预报误差,形势场的预报效果也得到一定改善。C-P边界层方案的应用提升了GRAPES全球模式的总体预报性能。Abstract: It is an important challenge in numerical weather and climate prediction to obtain accurate coupling between physical parameterization and high resolution dynamic framework. Increased resolution in models and the use of large time-steps in semi-Langrangian advection stress the need for an equally accurate computation in time of the corresponding physical parameterizations and the physics-dynamics coupling on the temporal aspects. Physics-dynamics coupling on spatial aspects also plays a very important role on the accuracy of model predictions, for there is a choice for how to vertically arrange the predicted variables, namely, the Lorenz and Charney-Phillips grids.The physics-dynamics coupling on spatial aspects in GRAPES model is studied. As the Charney-Philips grid is used, the horizontal velocity is staggered relative to potential temperature, which means potential temperature and water substances are calculated at full levels, while horizontal velocity is calculated at half levels. In Lorenz physics scheme, all variables are set at half levels and the correspondent tendencies are estimated at half levels. The interpolation has to be used between full and half levels in physics-dynamics coupling before and after physics scheme package is called. The interpolation error is unavoidable and an unexpected zigzag noise appears because of the second-order difference in PBL (planetary boundary layer) scheme.In C-P PBL scheme, the momentum diffusivity KM is required at full levels and the heat diffusivity KH is required at half levels. It is easy to compute KM and KH in unstable PBL because KM and KH depend on the PBL height and surface variables. For local scheme in stable PBL and free convective atmosphere, diffusivities are functions of local Richardson number which has relation with both potential temperature and horizontal velocity. Here potential temperature gradient is averaged so that Richardson number is calculated at full levels. KM can be calculated at the full level and KH can be averaged at the half level. The boundary condition is given by the surface flux according to the constant flux layer. C-P PBL parameterization is developed to assure the accurate coupling of PBL physics and vertical Charney-Phillips grid.Improvements are detected using C-P PBL parameterization spatial physics-dynamics coupling in GRAPES_GFS model. The zigzag noise of temperature and moisture in PBL is removed and the correspondent profiles appear to be smooth with C-P PBL parameterization. The accuracy of PBL and dynamics coupling is improved, and an overall enhancement is found in the forecast of height and temperature.
-
Key words:
- GRAPES model;
- planetary boundary layer;
- Charney-Phillips grid;
- Lorenz grid
-
表 1 边界层方案变量在C-P和Lorenz垂直格点上的分布
Table 1 C-P and Lorenz configurations of variables in PBL scheme
垂直层次 C-P Lorenz n=N(上边界) θ, q n=N-0.5 u, v, KH θ, q, u, v ┋ ┋ ┋ n=1.5 u, v, KH θ, q, u, v n=1 θ, q,KM KH, KM n=0.5 u, v, (w′θ′)sKH θ, q, u, v n=0(地表) θ, q, u* w′θ′s, u* -
[1] Wedi N P.The Numerical Coupling of the Physical Parametrizations to the Dynamical Equations in a Forecast Model.Tech Memo, ECMWF:Reading, 1999. [2] Staniforth A, Wood N, Cote J.Analysis of the numerics of physics-dynamics coupling.Q J R Meteorol Soc, 2002, 128:2779-2799. doi: 10.1256/qj.02.25 [3] Staniforth A, Wood N, Cote J.A simple comparison of four physics-dynamics coupling schemes.Mon Wea Rev, 2002, 130:3129-3135. doi: 10.1175/1520-0493(2002)130<3129:ASCOFP>2.0.CO;2 [4] Cullen M J P, Salmond D J.On the use of a predictor-corrector scheme to couple the dynamics with the physical parametrizations in the ECMWF model.Q J R Meteorol Soc, 2003, 129:1217-1236. doi: 10.1256/qj.02.12 [5] Lorenz E N.Energy and numerical weather prediction.Tellus, 1960, 12:364-373. doi: 10.1111/tus.1960.12.issue-4 [6] Charney J G, Phillips N A.Numerical integration of the quasi-geostrophic equations for barotropic and simple baroclinic flows.J Meteorol, 1953, 10:71-99. doi: 10.1175/1520-0469(1953)010<0071:NIOTQG>2.0.CO;2 [7] Cullen M J P.The Use of Dynamical Knowledge of the Atmosphere to Improve NWP Models//Proceedings of ECMWF Workshop on Recent Development in Numerical Methods for Atmospheric Modeling.Reading, UK:Shinfield Park, 1999:418-441. [8] 陈德辉, 沈学顺.新一代数值预报系统GRAPES研究进展.应用气象学报, 2006, 17(6):773-777. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200606125&flag=1 [9] 伍湘君, 金之雁, 黄丽萍, 等.GRAPES模式软件框架与实现.应用气象学报, 2005, 16(4):539-546. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20050468&flag=1 [10] 黄丽萍, 伍湘君, 金之雁.GRAPES模式标准初始化方案设计与实现.应用气象学报, 2005, 16(3):374-384. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20050346&flag=1 [11] 胡江林, 沈学顺, 张红亮, 等.GRAPES模式动力框架的长期积分特征.应用气象学报, 2007, 18(3):276-284. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20070349&flag=1 [12] 陈德辉, 薛纪善, 杨学胜, 等.GRAPES新一代全球/区域多尺度统一数值预报模式.科学通报, 2008, 53(20):2395-2407. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200820002.htm [13] 徐国强, 陈德辉, 张红亮, 等.GRAPES模式中物理过程时间计算精度对降水预报的影响.大气科学, 2010, 34(5):875-881. http://www.cnki.com.cn/Article/CJFDTOTAL-DQXK201005002.htm [14] 薛纪善, 陈德辉.数值预报系统GRAPES的科学设计与应用.北京:科学出版社, 2008:103-104;383. [15] 薛纪善.新世纪初我国数值天气预报的科技创新研究.应用气象学报, 2006, 17(5):602-610. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=200605103&flag=1 [16] 徐国强, 陈德辉, 薛纪善, 等.GRAPES物理过程的优化试验及程序结构设计.科学通报, 2008, 53(20):2428-2434. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200820006.htm [17] 苏勇, 沈学顺, 张倩, 等.应用样条插值提高GRAPES模式物理过程反馈精度.应用气象学报, 2014, 25(2):202-211. http://qikan.camscma.cn/jams/ch/reader/view_abstract.aspx?file_no=20140210&flag=1 [18] Holdaway D, Thuburn J, Wood N.Comparison of Lorenz and Charney-Phillips vertical discretisations for dynamics-boundary layer coupling.Part Ⅰ:Steady states.Q J R Meteorol Soc, 2013, 139:1073-1086. doi: 10.1002/qj.2016 [19] Holdaway D, Thuburn J, Wood N.Comparison of Lorenz and Charney-Phillips vertical discretisations for dynamics-boundary layer coupling.PartⅡ:Transients.Q J R Meteorol Soc, 2013, 139:1087-1098. doi: 10.1002/qj.2017 [20] Troen I, Mahrt L.A simple model of the atmospheric boundary layer sensitivity to surface evaporation.Bound Layer Metero, 1984, 37:129-148. https://www.researchgate.net/profile/Larry_Mahrt/publication/226452404_A_simple_model_of_the_atmospheric_boundary_layer_Sensitivity_to_surface_evaporation/links/57cc97cd08ae59825185dc28.pdf?origin=publication_detail [21] Hostlag A A M, Moeng C H.Eddy diffusivity and countergradient transport in the convective atmospheric boundary layer.J Atmos Sci, 1991, 48:1690-1698. doi: 10.1175/1520-0469(1991)048<1690:EDACTI>2.0.CO;2 [22] Hong S Y, Pan H L.Nonlocal boundary layer vertical diffusion in a medium-range forecast model.Mon Wea Rev, 1996, 124:2322-2339. doi: 10.1175/1520-0493(1996)124<2322:NBLVDI>2.0.CO;2 [23] Lock A P, Brown A R, Bush M R, et al, A new boundary layer mixing scheme.Part Ⅰ:Scheme description and single-column model test.Mon Wea Rev, 2000, 128:3187-3199. doi: 10.1175/1520-0493(2000)128<3187:ANBLMS>2.0.CO;2 [24] Han J, Pan H L.Revision of convection and vertical diffusion schemes in the NCEP global forecast system.Wea Forecasting, 2010, 26:520-533. https://www.researchgate.net/publication/270719453_Revision_of_Convection_and_Vertical_Diffusion_Schemes_in_the_NCEP_Global_Forecast_System?_sg=WbxXX6lYPoBW24q5ORLXr-Z9ZSH1liNkuIWmoqslyvNpiQiPZkqAD5XeUeUfCyr4wtd09HIxVsEdUs-157EEEw [25] Lorenz E N.Deterministic non-periodical flow.J Atmos Sci, 1963, 20:130-141. doi: 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 -

 设为首页
设为首页 加入收藏
加入收藏


 下载:
下载: